Cara Menentukan Himpunan Penyelesaian Sistem Pertidaksamaan Kuadrat Dua Variabel (Sptdlkdv)

Hallo temen-temen???

Pertama-tama gue ucapin trimakasih buat para pengunjung weblog gue :). Slamat datang di weblog paling bermanfaat sedunia.

Dan gue doaian semoga orang-orang yang ngunjungin weblog gue pada masuk surga semua, trs selama hidupnya selalu di beri kemudahan, trs all the best deh buat kalian :D

Udah kaya ulang tahun aja ya ???.... Sorry ya klo penulis suka bercanda :)

Kembali lagi bersama gue muhamad pajar sidik, gue adalah seorang penulis blogger yang ganteng dan baik hati :D cieeee.....

Di hari yang indah ini alhamdulillah gue bisa nulis artikel kembali, yang mudah-mudahan artikel ini bisa bermanfaat buat kalian semua.

Kali ini gue bakalan nulis artikel Cara Menentukan Himpunan Penyelesaian Sistem Pertidaksamaan Kuadrat Dua Variabel (SPtdLKDV), Tanpa panjang lebar lagi yo depository fiscal establishment gibe it out

Cara Menentukan Himpunan Penyelesaian Sistem Pertidaksamaan Kuadrat Dua Variabel (SPtdLKDV)

Sebelum ke langkah-langkah untuk menentukan himpunan penyelesaian pertidaksamaan kuadrat dua variabel, alangkah baiknya teman-teman mengenal dahulu bentuk umum dari pertidaksaman linier kuadrat dua variabel.

Bentuk Umum Pertidaksamaan Kuadrat Dua Variabel

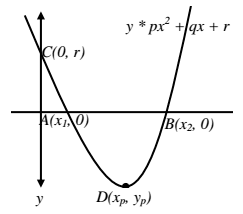
y * px² + qx + r

Keterangan :

y dan x : Variabel

p dan q : Koefisien

r : Konstanta

* : Tanda pertidaksamaan (<, <, >, dan >)

Sekarang kita lanjut ke langkah-langkah cara menentukan himpunan penyelesaian pertidaksamaan kuadrat dua variabel.

Langkah - Langkah Cara Menentukan Himpunan Penyelesaian Sistem Pertidaksamaan Kuadrat Dua Variabel (SPtdLKDV)

Langkah ke-1 :

Menentukn titik potong sumbu-x, dimana y = 0

y = px² + qx + r

0 = px² + qx + r

Lihat nilai diskriminanya terlebih dahulu {D = (q)² - iv . (p) . (r)}

• Jika D < 0 ; (nilai D Negatif) tidak memiliki titik potong terhadap sumbu-x, sehingga tidak perlu dilanjutkan
• Jika D = 0 ; hanya memiliki satu titik potong terhadap sumbu-x (titik balik pada sumbu x), dilanjutkan dengan mencari titik potongnya dengan menggunakan pemfaktoran, melengkapkan kuadrat sempurna, atau rumus abc. Koordinat yang diperoleh hanya satu A(x₁, 0),
• Jika D > 0 ; (nilai D positif) memiliki dua titik potong terhadap sumbu-x, dilanjutkan dengan mencari titik potongnya dengan menggunakan pemfaktoran, lelengkapkan kuadrat sempurna, atau rumus abc.

Rumus abc = x_1.2 = (-(q) + √(q)² - 4(p)(r))/2(p)

Diperoleh titik A(x₁, 0) dan B(x_2, 0).

Langkah ke-2 :

Menentukan titik potong sumbu-y, dimana x = 0

y = px² + qx + r

y = p(0)² + q(0) + r

y = r

Maka diperoleh titik C(0, r)

Langkah ke-3

Menentukan titik balik (x_p, y_p)

x_p = - q/(2p)

y p = D/(-4p) = (q² - 4pr)/(-4p)

Diperoleh titik (x_p, y_p)

Langkah ke-4

Menentukan beberapa titik yang lain :

y = px² + qx + r

Ctt : ambil nilai x di atas dan di bawah x_p

Langkah ke-5 :

Tinggal menentukan daerah himpunan penyelesaian dengan cara mengambil satu titik (yang ada di atas garis atau di bawah garis y = px² + qx + r) dan disubstitusikn ke pertidaksamaan y * px² + qx + r.

Daerah HP yang tidak diarsir.

Sekian artikel kali ini. Mohon maaf apabila ada salah-salah kata.

Akhir kata wassalamualikum wr. wb.

Cara Mencari Himpunan Penyelesaian Pertidaksamaan Kuadrat

Hallo temen-temen???

Pertama-tama gue ucapin trimakasih buat para pengunjung spider web log gue :). Slamat datang di spider web log paling bermanfaat sedunia.

Dan gue doaian semoga orang-orang yang ngunjungin spider web log gue pada masuk surga semua, trs selama hidupnya selalu di beri kemudahan, trs all the best deh buat kalian :D

Udah kaya ulang tahun aja ya ???.... Sorry ya klo penulis suka bercanda :)

Kembali lagi bersama gue muhamad pajar sidik, gue adalah seorang penulis blogger yang ganteng dan baik hati :D cieeee.....

Di hari yang indah ini alhamdulillah gue bisa nulis artikel kembali, yang mudah-mudahan artikel ini bisa bermanfaat buat kalian semua.

Kali ini gue bakalan nulis artikel tentang cara mencari himpunan penyelesaian pertidaksamaan kuadrat, Tanpa panjang lebar lagi yo banking concern tally it out !

Hal yang paling penting dalam materi pertidaksamaan kuadrat yaitu menentukan himpunan penyelesaiannya. Apa itu himpunan penyelesaian??? Himpunan penyelesaian ialah sebuah himpunan hasil penyelesaian dari suatu pertidaksamaan. Mencari Himpunan penyelesaian dikhususkan hanya pada materi pertidaksamaan, karena untuk materi persamaan sudah memiliki satu jawaban pasti. Dalam mencari himpunan penyelesaian dari pertidaksamaan kuadrat, tentunya ada beberapa langkah tertentu, diantaranya :

1. Ubah pertidaksamaan kuadrat se-olah-olah menjadi persamaan kuadrat
2. Cari akar akar dari pertidaksamaan kuadrat yang sudah diubah menjadi persamaan kuadrat
3. Menentukan himpunan penyelesaiannya dengan uji coba dengan bilangan 0

1. Ubah pertidaksamaan kuadrat se-olah-olah menjadi persamaan kuadrat

Untuk langkah yang pertama yaitu mengubah dahulu pertidaksamaan kuadrat, menjadi persamaan kuadrat, dengan tujuan untuk mempermudah pengerjaan. Kita ambil contoh soal :

Contoh :

Tentukanlah himpunan penyelesaian dari x² + x -6  > 0 !

Nah untuk menjawab soal yang seperti ini, untuk langkah pertama hanya kita ubah dulu ke persamaan kuadrat, yaitu menjadi :

x² + x -6  = 0. Nah dalam bentuk persamaan kita akan lebih ringan untuk mengerjakannya.

2. Cari akar akar dari pertidaksamaan kuadrat yang sudah diubah menjadi persamaan kuadrat

Nah pada langkah kedua yaitu kita cari akar-akar dari pertidaksamaan kuadrat yang telah di ubah ke persamaan kuadrat. Caranya bisa kita cari dengan cara pemfaktoran. Maka :

x² + x -6  = 0

Untuk mencari faktor kita cari bilangan yang apabila ditambahkan hasilnya menjadi i dan apabila dikalikan menjadi -6. dan bilangan tersebut adalah :

three dan -2. Maka faktor dari x² + x -6  = 0 adalah :

(x - 2)(x + 3) = 0. Maka akar akarnya adalah :

x - ii = 0

x = 2

dan :

x + three = 0

x = -3

Jadi akar akar dari x² + x -6  = 0 adalah ii dan -3

3. Menentukan himpunan penyelesaiannya dengan uji coba bilangan 0

Dan yang terakhir kita menentukan berapa sajakah himpunan penyelesaiannya. Caranya dengan menguji coba pertidaksamaan dengan bilangan 0.

x² + x - half dozen  > 0 kemudian kita ganti x dengan bilangan 0, menjadi :

0² + 0 - half dozen  > 0

-6  > 0

Dan hasil ujinya bernilai salah, karena -6 itu tidak lebih besar dari pada 0, akan tetapi sebaliknya. Dan artinya himpunan penyelesaianpun tidak boleh melibatkan bilangan 0. Karena akar-akar dari x² + x - half dozen  > 0 adalah ii dan -3, ini artinya himpunan penyelsainnya dibatasi dengan bilangan ii dan -3. Karena bilangan nol bukanlah bagian dari himpunan penyelesaian, maka :

Hp = {x│x < -3 dan x > 2} atau Hp = { x = -3, -4, -5,.....  dan x = 2, 3, 4,.... }

Kesimpulan

Jadi untuk mencari himpunan penyelesaian itu ada cara cara tertentu, di antaranya :

1. Ubah pertidaksamaan kuadrat se-olah-olah menjadi persamaan kuadrat
2. Cari akar akar dari pertidaksamaan kuadrat yang sudah di ubah menjadi persamaan kuadrat
3. Menentukan himpunan penyelesaiannya dengan uji coba bilangan 0

Dengan cara tersebut kita dapat menemukan himpunan penyelesaian dari pertidaksamaan kuadrat dengan mudah dan efektif.  

Sekian dulu artikel kali ini. Mohon maaf apabila ada salah-salah kata

Akhir kata wassalamualaikum wr. wb.