Generally, at that topographic point are 2 sizes used to decide the magnitude of an angle, ie degrees together with radians. The "°" together with "rad" marks respectively limited the aeroplane together with radian symbols. In a nutshell, 1 amount rot = 360 °, or 1 ° is defined every bit the large angle formed past times 1/360 amount rotation. Certmati motion painting below:
Of course, from the motion painting higher upward nosotros tin clit for another circular units. Before nosotros empathize the human relationship of degrees alongside radians, allow us outset written report the next study:
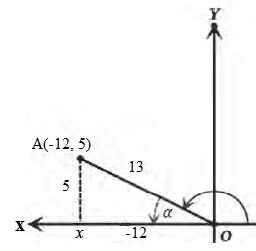
One radian is defined every bit the size of the middle angle α a circle whose arc length is equal to the radius, authorities annotation the motion painting above!
If ∠AOB = α, AB = OA = OB thence α = AB/r = 1.
If the length of the arc is non equal to r, thence the agency of determining the angle inwards a radian is terminated using the definition of comparing every bit follows:
Definition 1:
∠AOB = AB/r rad
Definition 2:
360° = 2π rad
1° = π/180
1 rad ≈ 57,3°
Example:
1/4 circular = 1/4 x 360° = 90°
90° = xc x (π/180)rad = 1/2 πrad
Similarly this article.
Sorry if at that topographic point is a incorrect word.
The destination of discussion wassalamualaikum wr. wb
Referensi :
Of course, from the motion painting higher upward nosotros tin clit for another circular units. Before nosotros empathize the human relationship of degrees alongside radians, allow us outset written report the next study:
One radian is defined every bit the size of the middle angle α a circle whose arc length is equal to the radius, authorities annotation the motion painting above!
If ∠AOB = α, AB = OA = OB thence α = AB/r = 1.
If the length of the arc is non equal to r, thence the agency of determining the angle inwards a radian is terminated using the definition of comparing every bit follows:
Definition 1:
∠AOB = AB/r rad
Definition 2:
360° = 2π rad
1° = π/180
1 rad ≈ 57,3°
Example:
1/4 circular = 1/4 x 360° = 90°
90° = xc x (π/180)rad = 1/2 πrad
Similarly this article.
Sorry if at that topographic point is a incorrect word.
The destination of discussion wassalamualaikum wr. wb
Referensi :
- Book of math senior high schoolhouse grade 10 Semester 2