Hallo temen-temen???
Pertama-tama gue ucapin trimakasih buat para pengunjung weblog gue :). Slamat datang di weblog paling bermanfaat sedunia.
Dan gue doaian semoga orang-orang yang ngunjungin weblog gue pada masuk surga semua, trs selama hidupnya selalu di beri kemudahan, trs all the best deh buat kalian :D
Udah kaya ulang tahun aja ya ???.... Sorry ya klo penulis suka bercanda :)
Kembali lagi bersama gue muhamad pajar sidik, gue adalah seorang penulis blogger yang ganteng dan baik hati :D cieeee.....
Di hari yang indah ini alhamdulillah gue bisa nulis artikel kembali, yang mudah-mudahan artikel ini bisa bermanfaat buat kalian semua.
Kali ini gue bakalan nulis artikel tentang Cara Menentukan Daerah Himpunan Penyelesaian Pertidaksamaan Linier Dua Variable, Tanpa panjang lebar lagi yo banking concern agree it out !
Cara Menentukan Daerah Himpunan Penyelesaian Pertidaksamaan Linier Dua Variable
Pertidaksamaan linier dua variabel, yaitu pertidak samaan yang memuat dua peubah misalnya x dan y. Himpunan penyelesaian pertidaksamaan tersebut dapat disaikan dalam bidang cartesius. Bentuk-bentuk pertidaksamaan linier adalah :
ax + yesteryear < c, ax + yesteryear < c, ax + yesteryear > c atau ax + yesteryear > c.
Langkah-langkah yang ditempuh untuk menyelesaikan daerah himpunan pertidaksamaan linier dua variabel adalah sebagai berikut :
1. Gambarlah garis ax + yesteryear = c pada bidang cartesius dengan cara mencari titik-titik potong grafik dengan sumbu x (y = 0) dan sumbu y (x = 0).
2. Ambil titik sembarang P(x1, y1) yang bukan terletak pada garis tersebut, kemudian dihitung nilai dari ax1 + by1. Nilai ax1 + by1 ini dibandingkan dengan nilai c.
3. Daerah penyelesaian untuk pertidaksamaan ax + yesteryear < c ditentukan sebagai berikut :
- Jika ax1 + by1 < c, maka daerah yang memuat P merupakan daerah penyelesaian.
- Jika ax1 + by1 > c, maka daerah yang memuat titik P bukan merupakan daerah penyelesaian.
4. Daerah penyelesaian untuk petidaksamaan ax + yesteryear > c ditentukan sebagai berikut :
- Jika ax1 + by1 > c, maka daerah yang memuat P merupakan daerah penyelesaian.
- Jika ax1 + by1 < c, maka daerah yang memuat titik P bukan merupakan daerah penyeleasian.
5. Daerah yang bukan merupakan penyelesaian diberi arsiran, sehingga daerah penyelesaiannya merupakan daerah tanpa arsiran. Hal ini sangat membantu pada saat menentukan daerah yang memenuhi terhadap beberapa pertidaksamaan.
6. Daerah penyelesaian untuk pertidaksamaan yang memuat tanda sama dengan digambar dengan garis penuh, sedangkan daerah penyelesaian pertidaksamaan yang tidak memuat tanda sama dengan digambar dengan garis putus-putus.
Contoh:
Tentukan daerah penyelesaian dari 2x + y < 4 !!!
Jawaban :
2x + y = 4
Untuk mencari titik potong grafik dengan sumbu x dan sumbu y dicari dengan cara membuat tabel berikut ini :
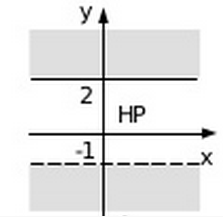
Dengan demikian titik potong dengan sumbu x dan y adalah (2, 0) dan (0, 4). Ambilah titik P(0, 0) sebagai titik uji pada 2x + y < 4 dan diperoleh 2.0 + 0 < 4. Daerah yang terdapat titik P merupakan penyelesaian (daerah tidak terarsir) :
Jawaban :
2x + y = 4
Untuk mencari titik potong grafik dengan sumbu x dan sumbu y dicari dengan cara membuat tabel berikut ini :
Dengan demikian titik potong dengan sumbu x dan y adalah (2, 0) dan (0, 4). Ambilah titik P(0, 0) sebagai titik uji pada 2x + y < 4 dan diperoleh 2.0 + 0 < 4. Daerah yang terdapat titik P merupakan penyelesaian (daerah tidak terarsir) :
Sekian artikel kali ini. Mohon maaf apabila ada salah-salah kata.
Akhir kata wassalamualaikum wr. wb.
Saya sarankan untuk membaca juga artikel :
Saya sarankan untuk membaca juga artikel :
- Cara Menentukan Himpunan Penyelesaian Pertidaksamaan Linier Satu Variabel
- Sistem Pertidaksamaan Linear Dua Variable
- Sistem Pertidaksamaan Linear Satu Variable
- Soal Aplikasi Pertidaksamaan Linear dan Pembahasan
- Cara Menentukan Nilai Optimum dengan Garis Selidik
- Cara Menentukan Nilai Optimum Dengan Uji Titik Pojok
- Cara mengubah Soal Cerita Menjadi Model Matematika
- Contoh Grafik Himpunan Penyelesaian Sistem Pertidaksamaan Linier Satu Variabel
- Program Linear
Referensi :
- Buku kelas 10 matematika SMK Bisnins dan Management karangan To'ali