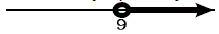Hallo temen-temen???
Pertama-tama gue ucapin trimakasih buat para pengunjung spider web log gue :). Slamat datang di spider web log paling bermanfaat sedunia.
Dan gue doaian semoga orang-orang yang ngunjungin spider web log gue pada masuk surga semua, trs selama hidupnya selalu di beri kemudahan, trs all the best deh buat kalian :D
Udah kaya ulang tahun aja ya ???.... Sorry ya klo penulis suka bercanda :)
Kembali lagi bersama gue muhamad pajar sidik, gue adalah seorang penulis blogger yang ganteng dan baik hati :D cieeee.....
Di hari yang indah ini alhamdulillah gue bisa nulis artikel kembali, yang mudah-mudahan artikel ini bisa bermanfaat buat kalian semua.
Kali ini gue bakalan nulis artikel tentang Cara Menentukan Himpunan Penyelesaian Pertidaksamaan Linier Satu Variabel, Tanpa panjang lebar lagi yo banking company gibe it out !
Cara Menentukan Himpunan Penyelesaian Pertidaksamaan Linier Satu Variabel
Bentuk umum petidaksamaan linier satu variabel dinyatakan dengan :
ax + b (R) 0; a, b ∈ Rill dan (R) = Salah satu relasi pertidaksamaan
Cara menentukan himpunan penyelesaian pertidaksamaan linier satu variabel hampir sama dengan cara menentukan persamaan linier satu variabel.
Himpunan penyelesaian pertidaksamaan biasanya juga dituliskan dalam bentuk interval atau selang. Beberapa bentuk atau jenis interval disajikan sebagai berikut :
Tanda ● pada batas interval berarti batas tersebut termasuk dalam interval. Sedangkan tanda ◌ pada batas interval berarti batas tersebut tidak termasuk dalam interval. Beberapa hal yang perlu diperhatikan dalam menyelesaikan pertidaksamaan adalah sebagai berikut :
- Tanda pertidaksamaan tidak berubah arah jika pada ruas kiri dan kanan ditambah atau dikurangkan dengan bilangan negatif atau bilangan positif yang sama. (Sifat 1)
- Tanda pertidaksamaan tidak berubah arah jika pada ruas kiri dan kanan dikalikan atau dibagi dengan bilangan positif yang sama. (Sifat 2)
- Tanda pertidaksamaan berubah arah atau dibalik jika pada ruas kiri dan kanan dikalikan atau dibagi dengan bilangan negatif yang sama. (Sifat 3)
Contoh :
Tentukan himpunan penyelesaian dari 5x > 4x + 9 !!!
Jawab :
5x > 4x + 9
5x - 4x > 4x + nine - 4x (Sifat 1)
x > nine
Jadi Himpunan penyelesaiannya adalah {x │ x > 9}, dengan garis bilangan :
Jawab :
5x > 4x + 9
5x - 4x > 4x + nine - 4x (Sifat 1)
x > nine
Jadi Himpunan penyelesaiannya adalah {x │ x > 9}, dengan garis bilangan :
Sekian artikel kali ini. Mohon maaf apabila ada salah-salah kata.
Akhir kata wassalamualaikum wr. wb.
Saya sarankan untuk membaca juga artikel :
Saya sarankan untuk membaca juga artikel :
Referensi :
- Buku matematika SMK Bisnis dan Management kelas 10 karangan To'ali.