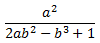Hallo temen-temen???
Pertama-tama gue ucapin trimakasih buat para pengunjung spider web log gue :). Slamat datang di spider web log paling bermanfaat sedunia.
Dan gue doaian semoga orang-orang yang ngunjungin spider web log gue pada masuk surga semua, trs selama hidupnya selalu di beri kemudahan, trs all the best deh buat kalian :D
Udah kaya ulang tahun aja ya ???.... Sorry ya klo penulis suka bercanda :)
Kembali lagi bersama gue muhamad pajar sidik, gue adalah seorang penulis blogger yang ganteng dan baik hati :D cieeee.....
Di hari yang indah ini alhamdulillah gue bisa nulis artikel kembali, yang mudah-mudahan artikel ini bisa bermanfaat buat kalian semua.
Kali ini gue bakalan nulis artikel tentang Soal Olimpiade Matematika Tingkat Internasional, Tanpa panjang lebar lagi yo banking corporation lucifer it out !
Soal Olimpiade Matematika Tingkat Internasional
Version : English
First day
Tokyo, July thirteen 2003
Problem 1. Let A hold out a subset of the ready S = {1, 2, ...., 1000000} containing just 101 elements. Prove that at that topographic point be numbers t1, t2, ..., t100 inward S such that the sets :
Aj = {x + tj | x ∈ A} for j = 1, 2, ..., 100
are pairwise disjoint.
Problem 2. Determine all pairs of positive integers (a, b) such that
is a positif integer.
Problem 3. H5N1 convex hexagon is given inward which whatever 2 contrary sides convey the next properti : the distance betwixt their midpoints is √3/2 times the amount of their lenghts. Prove that all the angels of the hexagon are equal.
(A convex hexagon ABCDEF has 3 pairs of contrary sides : AB together with DE, BC together with EF, CD together with FA.)
Second day
Tokyo, July 14, 2003
Problem 4. Let ABCD hold out a cyclic quardrilaterial. Let P, Q together with R hold out the feet of the perpendiculars from D to lines BC, CA together with AB respectively. Show that PQ = QR if together with solely if the besectors of ∠ABC together with ∠ADC reckon on AC.
Problem 5. Let n hold out a positive integer and x1, x2, ..., xn hold out existent numbers amongst x1 < x2 < .... xn.
(a) Prove that :
(b) Show that equality holds if together with solely if 1, x2, ..., xn is an arithmatic sequence.
Problem 6. Let p hold out a prime number. Prove that at that topographic point be a prime let on q such that for every integer n, the let on np-p is non divisible past times q.
Sekian artikel kali ini. Mohon maaf apabila ada salah-salah kata.
Akhir kata wassalamualaikum wr. wb.
Referensi :
- Buku Olimpiade matematika (Wono Setya Budhi)