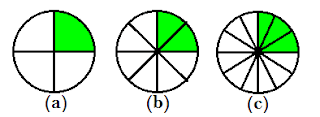Home Posts filed under Pecahan
Showing posts with label Pecahan. Show all posts
Showing posts with label Pecahan. Show all posts

Bilangan Pecahan

Hallo temen-temen???
Kali ini gue bakalan sahre materi tentang Bilangan Pecahan. Yo simak!

Pengertian Bilangan Pecahan

Ibu mempunyai xx buah jeruk yang akan dibagikan pada three orang anak, adi memperoleh iv buah jeruk, fitri memperoleh v buah jeruk, dan ketut memperoleh 10 buah jeruk. Adapun sisanya disimpan oleh ibu. Dalam hal ini, Adi memperoleh 4/20 bagian jeruk, Fitri memperoleh 5/20 bagian jeruk, dan ketut memperoleh 10/20 bagian jeruk. Apakah menurutmu sisa yang disimpan oleh ibu 1/20 bagian jeruk ?
Bilangan-bilangan 4/20, 5/20, 10/20, dan 1/20 yang merupakan banyak buah jeruk dibandingkan jumlah keseluruhan buah jeruk disebut bilangan pecahan. Bilangan-bilangan pecahan sering disebut sebagai pecahan saja. Pada pecahan tersebut, angka-angka 4, 5, 10, dan i disebut pembilang, sedangkan angka xx disebut penyebut.
Dari urain di atas, dapat dikatakan bahwa pecahan merupaka bagian dari keseluruhan.
Sekarang perhatikan gambar di atas!
Luas daerah warna hijau pada gambar di atas (a) menunjukan pecahan 1/3
Luas daerah warna hijau pada gambar di atas (b) menunjukan pecahan 3/6
Luas daerah warna hijau pada gambar di atas (c) menunjukan pecahan 3/12
Luas daerah warna hijau pada gambar di atas (d) menunjukan pecahan 5/24
Berdasarkan uraian di atas, dapat disimpulkan sebagain berikut :
Bilangan pecahan adalah bilangan yang dapat dinyatakan sebagai p/q, dengan p,q bilangan bulat dan q tidak sama dengan 0. Bilangan p disebut pembilangan dan bilangan q  disebut penyebut.

2. Pecahan Senilai

Perhatikan Gambar di atas !
Luas daerah yang berwarna hijau (a) pada gambar di atas menunjukan 1/4 dari luas lingkaran.
Luas daerah yang berwarna hijau (b) pada gambar di atas menunjukan 2/8 dari luas lingkaran.
Luas daerah yang berwarna hijau (c) pada gambar di atas menunjukan 3/12 dari luas lingkaran.
Dari ketiga gambar tersebut, tampak bahwa daerah yang berwarna hijau memiliki luas yang sama. Hal ini berarti 1/4 = 2/8 = 3/12, selanjutnya, pecahan-pecahan 1/4, 2/8, dan 3/12 dikatakan sebagai pecahan-pecahan senilai.
Pecahan senilai adalah pecahan-pecahan yang benilai sama.
Untuk memperoleh pecahan yang senilai, pelajari uraian berikut!
1/3 = 1x2 / 3x2 = 2/6
1/3 = 1x3 / 3x3 = 3/9
1/3 = 1x4 / 3x4 = 4/12
2/6 = ii : ii / vi : ii = 1/3
3/9 = three : three / nine : three = 1/3
4/12 = iv :4 / 12 : iv = 1/3
5/15 = v : v / fifteen : v = 1/3
Pecahan - pecahan 1/3, 2/6, 3/9, 4/12, dan 5/15 di atas mempunyai nilai yang sama, sehingga dapat ditulis 1/3 = 2/6 =  3/9 = 4/12 = 5/15.
Dari uraian di atas, tampak bahwa untuk memperoleh pecahan-pecahan yang senilai dapat dilakukan dengan mengalikan atau membagi pembilang dan penyebut dengan bilangan yang sama.
Secara umum dapat dituliskan sebagai berikut :
Jika diketahui pecahan p/q dengan p , q tidak sama dengan 0 maka berlaku p/q = p x a / q x a  atau p/q = p : b / q : b,  di mana a, b, konstanta positif bukan no.
Contoh :
Tentukan dua pecahan yang senilai dengan pecahan 2/3
Penyelesaian :
2/3 = ii x ii / three x ii = 4/6
2/3 = ii x v / three x v = 10/15

3. Menyederhanakan Pecahan

Kalian telah mengetahui cara menentukan pecahan senilai, yaitu dengan mengkalikan atau membagi pembilang dan pecahan dengan bilangan yang sama, kecuali nol (0).
Sekarang perhatikan cara menemukan pecahan pecahan senilai berikut :
24/36 = 24 : ii / 36 : ii = 12/18
24/36 = 24 : three / 36 : three = 8/12
24/36 = 24 : vi / 36 : vi = 4/6
24/36 = 24 : 12 / 36 : 12 = 2/3
Pecahan 2/3 pada pengerjaan di atas tidak dapat dibagi lagi dengan bilangan lain selain nol. Dalam hal ini, pecahan 2/3 merupakan bentuk paling sederhana 24/36.
Untuk memperoleh bentuk paling sederhana, pecahan 24/36 harus dibagi dengan bilangan 12. Coba cek apakan 12 adalah FPB dari bilangan 24 dan 36?
Suatu pecahan p/q, q tidak sama dengan 0 dapat disederhanakan dengan cara membagi pembilang dan penyebut pecahan tersebut dengan FPB nya. Hal ini dapat ditulis sebagai berikut.
Dalam menyederhanakan sebarang pecahan p/q, q tidak sama dengan 0, berlaku p/q = p : a / q : a, dimana a Faktor Persekutuan Terbesar (FPB) dari p dan q.
Contoh :
Nyatakan pecahan 18/45 dalam bentuk pecahan paling sederhana!
Penyelesaian :
FPB dari xviii dan 45 adalah 9.
18/45 = xviii : nine / 45 : nine = 2/5
Jadi, bentuk pecahan paling sederhana dari 18/45 adalah 2/5.

4. Menyatakan Hubungan Antara Dua Pecahan

Perhatikan gambar di atas !
Luas daerah berwarna hijau (a) pada gambar di atas menunjukan 1/3 dari luas keseluruhan. Adapun luas daerah berwarna hijau (b) menunjukan 2/3 dari keseluruhan. Tampak bahwa pada gambar di atas (b) lebih besar dari luas arsiran pada gambar (a) atau dapat ditulis 2/3 > 1/3 atau 1/3 < 2/3.
Dari uraian di atas dapat dikatakan bahwa untuk menyatakan hubungan dua pecahan, bandingkan pembilangnya, jika penyebut kedua pecahan sama. Adapun jika penyebut kedua pecahan berbeda, untuk membandingkan pecaha tersebut, samakan terlebih dahulu penyebut kedua pecahan (dengan menentukan KPK dan penyebut kedua pecahan), kemudian dibandingkan pembilangnya. Contoh :
berilah tanda > atau < untuk setiap pernyataan berikut sehingga menjadi pernyataan yang benar.
3/4 ... 2/3
Penyelesaian :
3/4 = 9/12
2/3 = 8/12
(KPK dari iv dan three adalah 12)
karena 9/12 > 8/12 maka 3/4 > 2/3 atau 2/3 < 3/4

5. Menentukan Letak Pecahan Pada Garis Bilangan

Pada bab sebelumnya kalian telah mempelajari letak bilangan bulat pada garis bilangan. Coba kalian ingat kembali garis bilangan pada bilangan bulat.
Pada garis bilangan, bilangan pecahan terletak di antara dua bilangan bulat. Sebagai contoh, jika pada garis bilangan di atas, jarak antara dua bilangan bulat yang berdekatan kalian bagi dua maka garis bilangannya menjadi :
Adapun untuk letak pecahan yang lain, dapat kalian tentukan dengan membagi jarak antara dua bilangan bulat menurut besarnya penyebut.
Pada garis bilangan, pecahan yang lebih besar berada di sebelah kanan, sedangkan pecahan yang lebih kecil berada di sebelah kiri. Perhatikan gambar di atas !
Pada garis bilangan di atas, tampak terdapat pecahan negatif. Pecahan negatif adalah pecahan yang nilainnya lebih kecil dari pada nol. Pecahan negarif menggunakan tanda negatif, misalnya :
-1/2, -1/3, -1/4, dan -3/5. Coba, Letakan pecahan -1/2, -1/3, -1/4, dan -3/5 pada garis bilangan.

6. Menentkan Pecahan Yang Nilainya di Antara Dua Pecahan

Misalkan, kita mempunyai pecahan 1/6 dan 2/6. Menurutmu, apakah ada bilangan pecahan yang terletak di antara pecahan 1/6 dan 2/6? Untuk menjawabnya, perhatikan bahwa 1/6 = 2/12 dan 2/6 = 4/12. Kita peroleh bahwa 2/12 < 3/12 < 4/12. Jadi, pecahan yang terletak di antara 1/6 dan 2/6 adalah 3/12.
Coba cek hal ini dengan menggambarnya pada garis bilangan.
Di antara dua pecahan yang berbeda selalu dapat ditemukan pecahan yang nilainya di antara dua pecaha tersebut.
Untuk menentukan pecahan yang nilainya di antara dua pecahan, langkah-langkahnya sebagai berikut.
  1. Samakan penyebut dari kedua pecahan. Kemudian, tentukan nilai pecahan yang terletak di antara kedua pecahan tersebut.
  2. Ubahlah lagi penyebutnya, jika belum diperoleh pecahan yang dimaksud. Begitu seterusnya.
Contoh :
Tentukan sebuah pecahan yang terletak di antara 3/5 dan 2/3!
Penyelesaian :
3/5 = three x three / v x three = 9/15
2/3 = ii x v / three x v = 10/15
Karena belum diperoleh pecahan yang dimaksud maka masing-masing penyebutnya diperbesar lagi sehingga diperoleh :
9/15 = nine x ii / fifteen x ii = 18/30
10/15 = 10 x ii / fifteen x 2  = 20/30
Di antara pecahan 18/30 dan 20/30 terdapat pecahan 19/30. Jadi, pecahan yang terletak di antara 3/5 dan 2/3 adalah 19/30.
Nah segini dulu ya artikel kali ini. Mohon maaf apabila ada kesalahan. Baca juga artkel lanjutannya yaitu tentang cara mengubah pecahan ke bentuk lain
Akhir kata wassalamualaikum wr. wb.
Materi ini dikutip dari buku matematika konsep dan aplikasinya karangan Dewi Nuharini dan Tri Wahyuni.

Cara Mengubah Pecahan Kebentuk Lain

Hallo teman-teman ????
Kali ini gue bakalan berbagi materi tentang Cara Mengubah Pecahan Kebentuk Lain . Yo simak !

1. Pecahan Sebagai Perbandingan Bagian dari Keseluruhan

Telah kalian ketahui bahwa pecahan merupakan bagian dari keseluruhan. Apabila terdapat dua besaran yang dibandingkan, pecahan dikatakan sebagai perbandingan bagian dari keseluruhan. Perhatikan contoh berikut :
Seorang anak memiliki 12 kelereng, yang terdiri atas iii kelereng warna merah, four kelereng warna hijau, dan v kelereng warna biru.
Tentukan perbandingan kelereng warna merah terhadap hijau !
Tentukan perbandingan kelereng warna merah terhadap biru!
Tentukan perbandingan kelereng warna hijau terhadap biru!
Penyelesaian :
a. Perbandingan kelereng warna merah terhadap hijau adalah 3/12 : 4/12 atau 1/4 : 1/3
b. Perbandingan kelereng warna merah terhadap biru adalah 3/12 : 5/12.
c. Perbandingan kelereng warna hijau terhadap biru adalah 4/12 : 5/12

2. Menyatakan Bilangan Bulat dalam Bentuk Pecahan

Perhatikan garis bilangan berikut :
Dari gambar di atas diperoleh :
0 = 0/2 = 0/3
i = 2/2 = 3/3
two = 4/2 = 6/3
iii = 6/2 = 9/3
four = 8/2 = 12/3
Berdasarkan uraian di atas dapat disimpulkan sebagai berikut :
Setiap bilangan bulat p,q dapat dinyatakan dalam bentuk pecahan p/q, dimana p merupakan kelipatan dari q,q tidak sama dengan 0.

3. Mengubah Pecahan Biasa Menjadi Pecahan Campuran dan Sebaliknya

Ibu memiliki iii buah apel yang akan dibagikan kepada two orang anaknya dengan sama besar. Bagian apel yang akan diperoleh tiap anak adalah satu apel dan setengah apel. Hal ini dapat dinyatakan sebagai iii : two atau
11/2 . Bentuk pecahan11/2 merupakan bentuk pecahan campuran. Pecahan campuran 11/2 terdiri dari atas bilangan bulat i dan bilangan pecahan 1/2.
Contoh :
Nyatakan pecahan 35/4 ke dalam pecahan campuran!
Penyelesaian :
Cara i :
35/4 = 35 dibagi 4. Hasilnya 35 : four = 8 sisa 3
35/4 = 83/4
Cara two :
35/4 = 32/4 + 3/4
35/4 = 8 + 3/4
35/4 = 83/4

4. Mengubah Bentuk Pecahan ke Bentuk Desimal dan Sebaliknya

Coba kalian ingat kembali mengenai nilai tempat pada bilangan pecahan desimal. Perhatikan nilai tempat pada bilangan 235,674 berikut :
four : Perseribuan, nilainya 4/1.000 atau 0,004
vii : Perseratusan, nilainya 7/100 atau 0,07
six : Persepuluhan, nilainya 6/10 atau 0,6
v : Satuan, nilainya 5
iii : Puluhan, nilainya 30
two : Ratusan, nilainya 200
Jika ditulis dalam bentuk panjang, diperoleh :
235,674 = 200 + thirty + v + 0,6 + 0,07 + 0,004
235,674 = 200 + thirty + v + 6/10 + 7/100 +4/1.000
235,674 = 200 + thirty + v + 600/1.000 + 70/1.000 +4/1.000
235,674 = 235 + 674/1.000
Apabila satuan pecahan biasa atau campuran akan diubah atau dinyatakan ke dalam bentuk pecahan desimal, maka dapat dilakukan dengan cara mengubah penyebutnya menjadi 10, 100, 1.000, 10.000, dan seterusnya. Dapat pula dengan cara membagi pembilang dengan penyebutnya.
Sebaliknya, untuk mengubah pecahan desimal menjadi pecahan biasa/campuran dapat kalian lakukan dengan menguraikan bentuk panjangnya terlebih dahulu.
Contoh :
Ubahlah pecahan 3/4 ke dalam bentuk pecahan desimal !
Penyelesaian :
Cara i :
3/4 = iii x 25 / four x 25 = 75/100 = 0,75
Jadi, 3/4 = 0,75

Cara two :
3/4 = iii : four = 0,75

Contoh :
Nyatakan bilangan 0,16 menjadi pecahan biasa/campuran yang paling sederhana !
Penyelesaian :
Cara i :
0,16 = 0 + 1/10 + 6/100
0,16 = 10/100 + 6/100
0,16 =16/100
0,16 =4/25
Cara two :
0,16 = 16/100
0,16 = sixteen : four / 100 : 4
0,16 =4/25

Perhatikan bentuk desimal 2,333....
Bentuk desimal seperti 2,333... disebut bentuk desimal berulang.
Untuk mengubah bentuk desimal berulang seperti di atas ke bentuk pecahan biasa dapat dilakukan dengan cara berikut.
Misalkan x = 2,333.... maka 10x = 23,333...
10x - x = 23,333... - 2,3....
9x = 21
x = 21/9
x = 7/3
jadi, 2,333... = 7/3

5. Mengubah Bentuk Pecahan ke Bentuk Persen dan Sebaliknya

Dapatkah kalian mengubah bentuk 2/5 dan 3/4 ke bentuk perseratus ?
2/5 = two x twenty / v x twenty = 40/100
3/4 = iii x 25 / four x 25 = 75/100
Bentuk pecahan perseratus seperti di atas disebut bentuk persen atau ditulis "%", sehingga 2/5 = 40/100 = 40% dan 3/4 = 75/100 = 75%
Dalam mengubah bentuk pecahan ke bentuk persen dapat dilakukan dengan cara mengubah pecahan semula menjadi pecahan senilai dengan penyebut 100. Jika hal itu sulit dikerjakan maka dapat dilakukan dengan cara mengalikan pecahan tersebut dengan 100%. Adapun untuk mengubah bentuk persen ke bentuk pecahan biasa/campuran, ubahlah menjadi perseratus, kemudian sederhanakannlah!
Contoh :
Nyatakan pecahan 7/8 dalam bentuk persen !
Penyelesaian :
7/8 = vii x 12,5 / 8 x 12,5 = 87,5/100 = 87,5 %

6. Mengubah Bentuk Pecahan ke Bentuk Permil dan Sebaliknya

Pecahan dalam bentuk perseribu disebut permil atau ditulis "0/00". Bentuk pecahan 275/1.000 dikatakan 275 permil dan ditulis 2750/00.
Dalam mengubah bentuk pecahan ke bentuk permil dapat dilakukan dengan mengubah pecahan semula menjadi pecahan senilai dengan penyebut 1.000. Jika hal ini sulit dikerjakan maka dapat dilakukan dengan mengalikan pecahan semula dengan 1.000 0/00 .
Contoh :
Nyatakan pecahan 17/20 dalam bentuk permil!
Penyelesaian :
17/20 = 17 x l / twenty x l = 850 / 1.000 = 850 0/00


Contoh :
Nyatakan bentuk permil 22,5 0/00!
Penyelesaian :
22,5 0/00 = 22,5 / 1.000 = 22,5 x two / 1.000 x two = 45 / 2.000 = 9/400
Nah segini dulu ya artikel kali ini. Mohon maaf apabila ada kesalahan. Baca juga artikel selanjutnya tentang Operasi Hitung Pecahan
Akhir kata wassalamualaikum wr. wb.
Materi ini dikutip dari buku matematika konsep dan aplikasinya karangan Dewi Nuharini dan Tri Wahyuni.

Operasi Hitung Pecahan

Hallo temen-temen!!!
Kali ini gue bakalan part materi tentang Operasi Hitung Pecahan. Yo simak !!

1. Penjumlahan dan Pengurangan Pecahan

a. Penjumlahan dan pengurangan pecahan dengan bilangan bulat.

Dalam menentukan hasil penjumlahan atau pengurangan pecahan dengan bilangan bulat, ubahlah bilangan bulat itu kedalam bentuk pecahan dengan penyebut sama dengan penyebut pecahan itu. Kemudian jumlahkan atau kurangkan pembilangnya sebagaimana pada bilangan bulat. Jika pecahan tersebut berbentuk pecahan campuran, jumlahkan atau kurangkan bilangan bulat itu dengan bagian bilangan bulat pada pecahan campuran.
Contoh :
Tentukan hasil penjumlahan dan pengurangan beriktut :
a. 2/5 + 3
b. 21/4 - three
Penyelesaian :
1. 2/5 + three = 2/5 + 15/5
    2/5 + three = (2 +15 )/5
    2/5 + three =  17/5
    2/5 + three =  32/5

2. Cara i : 
21/4 - three = (2-3) + 1/4
21/4 - three = -1+ 1/4
21/4 - three = -4/4 + 1/4
21/4 - three = -3/4
Cara ii :
21/4 - three = 9/4 - 3
21/4 - three = 9/4 -12/4
21/4 - three = -3/4

b. Penjumlahan dan Pengurangan Pecahan dengan Pecahan

Dalam menentukan hasil penjumlahan atau pengurangan dua pecahan, samakan penyebut kedua pecahan tersebut, yaitu dengan cara mencari KPK dari penyebut-penyebutnya. Kemudian, baru dijumlahkan atau dikurangkan pembilangnya.
Contoh :
Tentukan hasil dari 3/7 + 4/5!
Penyelesaian :
KPK dari v dan vii adalah 35, sehingga diperoleh :
3/7 + 4/5 = 15/35 + 28/35
3/7 + 4/5 = 43/35
3/7 + 4/5 = 18/35

c. Sifat-sifat pada penjumlahan dan pengurangan pecahan

Coba kalian ingat kembali sifat-sifat yang berlaku pada penjumlahan bilangan bulat.
Untuk setiap bilangan bulat a, b, dan c maka berlaku :
  1. Sifat tertutup : a + b = c ;
  2. Sifat komutatif : a + b = b + c ;
  3. Sifat asosiatif : (a+b) + c = a + (b+c) ; 
  4. Bilangan (0) adalah unsur identitas pada penjumlahan : a + 0 = 0 + a =  a ;
  5. Invers dari a adalah -a dan invers dari -a adalah a, sedemikian sehingga a + (-a) = (-a) + a = 0
Sifat-sifat tersebut juga berlaku pada penjumlahan bilangan pecahan, artinya sifat-sifat tersebut berlaku jika a, b, dan c bilangan pecahan. Coba buktikan hal ini dengan mendiskusikan bersama temanmu.

2. Perkalian Pecahan 

a. Perkalian pecahan dengan pecahan 

Untuk mengetahui cara menentukan hasil perkalian pada pecahan, perhatikan gambar di bawah ini:
Pada gambar di atas tampak bahwa luas yang berwarna hijau menunjukan pecahan 3/8 bagian dari luas keseluruhan.
Di pihak lain, daerah yang berwarna hijau menunjukan perkalian 1/2 x 3/4 = 3/8. Jadi dapat dikatakan bahwa luas daerah yang berwarna hijau sama dengan perkalian pecahan 1/2 x 3/4.
Dari uraian tersebut dapat disimpulkan sebagai berikut :
Untuk mengalikan dua pecahan p/q dan r/s dilakukan dengan mengkalikan pembilang dengan pembilang dan penyebut dengan penyebut atau dapat ditulis p/q x r/s = p x r / q x s dengan q, s tidak sama dengan 0.
Contoh :
Tentukan hasil perkalian dari 2/3 x 5/8 !
Penyelesaian :
2/3 x 5/8 = ii x v / three x 8 = 10/24 = 10 : ii / 24 : ii = 5/12

b. Sifat-sifat perkalian pada pecahan

Ingat kemballi sifat sifat yang berlaku pada perkalian bilangan bulat berikut :
Untuk setiap bilangan bulat a, b , dan c berlaku :
  1. Sifat tertutup : a x b = c ;
  2. Sifat komutatif : a x b = b x a ;
  3. Sifat asosiatif (a x b ) x c = a x ( b x c ) ;
  4. Sifat distributif perkalian terhadap penjumlahan :  a x ( b x c ) = (a x b) + (a x c) ;
  5. Sifat distributif perkalian terhadap pengurangan : a x ( b - c ) = (a x b) - (a x c) ;
  6. a x i = i x a = a ; bilangan i adalah unsur identitas pada perkalian.
Sifat - sifat ini juga berlaku pada perkalian bilangan pecahan .

c. Invers Pada Perkalian

Perhatikan perkalian bilangan berikut :
2/5 x 5/2 = 1
-3/8 x (-8/3) = 1
Pada perkalian-perkalian bilangan di atas, 2/5 adalah invers perkalian (kebalikan) dari 5/2. Sebaliknya, 5/2 adalah invers perkalian (kebalikan) dari 2/5.
Dari uraian tersebut dapat dikatakan bahwa hasil kali suatu bilangan dengan invers (kebalikan) bilangan itu sama dengan 1. Secara umum dapat dituliskan sebagai berikut :
  • Invers perkalian dari pecahan p/q adalah q/p atau invers perkalian dai q/p adalah p/q.
  • Suatu bilangan jika dikalikan dengan invers perkaliannya maka hasilnya sama dengan 1.

3. Pembagian Pecahan

Kalian telah mempelajari bahwa operasi pembagian pada bilangan bulat merupakan invers (kebalikan) dari perkalian. Hal ini juga berlaku pada pembagian bilangan pecahan.
Perhatikan uraian berikut :
3/2 : 7/12 = (3/2) / (2/12) = 3/2 x 12/7 = 36/14 = 18/7 = 24/7
Dengan maengamati uaraian di atas, secara umum dapat dinyatakan sebagai berikut :
Untuk sebarang pecahan p/q dan r/s dengan q tidak sama degan 0, r tidak sama dengan 0, s tidak sama dengan 0 berlaku p/q : r/s = p/q x s/r
Contoh :
Tentukan hasil pembagian bilangan 3/8 : 51/2
Penyelesaian :
3/8 : 51/2 = 3/8 : 11/2
3/8 : 51/2 = 3/8 : 2/11
3/8 : 51/2 = 3/4 : 1/11
3/8 : 51/2 = 3/44

4. Perpangkatan Pecahan

a. Bilangan pecahan berpangkat bilangan bulat positif

Pada pembahasan kali ini, kita hanya akan membahas perpangkatan pada pecahan dengan pangkat bilangan bulat positif . Di kelas IX nanti kalian akan mempelajari perpanggkatan pada pecahan dengan pangkat bilangan bulat negatif dan nol.
Pada bab sebelumnya, kalian telah mempelajari bahwa pada bilangan bulat berpangkat bilangan bulat positif berlaku :

An = a x a x a x.... x a, untuk setiap bilangan bulat a.
Dengan kata lain, perpangkatan merupakan perkalian burulang dengan bilangan yang sama. Defininsi tersebut juga berlaku pada bilangan pecahan berpangkat.
Perhatika uraian berikut :

(1/2)1 =1/2     
(1/2)2 =1/2 x 1/2 = 1/22 = 1/4


(1/2)3 =1/2 x 1/2 x 1/2 =1/23= 1/8
......
(1/2)n = 1/2 x 1/2 x ... x 1/2
Dari uraian di atas, secara umum dapat dituliskan sebagai berikut :
Untuk sebarang bilangan bulat p dan q dengan q tidak sama dengan 0 dan 1000 bilangan bulat positif berlaku.
(p/q)n = p/q x p/q x ... x p/q
Dalam hal ini, bilangan pecahan p/q disebut bilangan pokok.
Contoh :
Tentukan hasil operasi perpangkatan dari (-2/3)2!
Penyelesaian :
(-2/3)2 = (-2/3) x (-2/3) = (-2) x (-2) / three x three = 4/9

b. Sifat-sifat bilangan pecahan berpangkat

Coba kalian ingat kembali sifat-sifat pada bilangan bulat berpangkat bilangan bulat positif. Sifat-sifat tersebut juga berlaku pada bilangan pecahan sebagai berikut :
Untuk bilangan bulat p, q dengan q tidak sama dengan 0 dan m, n bilangan bulat positif berlaku sifat-sifat berikut :


(p/q)m = pm/qm
(p/q)m x (p/q)n = (p/q)m+n
(p/q)m : (p/q)n = (p/q)m-n
((p/q)m)n = (p/q)mxn

Contoh :
Tentukan nilai perpangkatan dari (2/3)5 : (2/3)2 !


(2/3)5 : (2/3)2 = (2/3)5-2
(2/3)5 : (2/3)2 = (2/3)3
(2/3)5 : (2/3)2 = (2/3) x (2/3) x (2/3)
(2/3)5 : (2/3)2 = 8/27

5. Operasi Hitung Campuran Pada Bilangan Pecahan.

Coba ingat kembali aturan-aturan yang berlaku pada operasi hitung campuran bilanga bulat berikut :
Apabila dalam suatu operasi hitung campuran bilangan bulat tidak terdapat tanda kurung, pengerjaannya berdasarkan sifat-sifat operasi hitung berikut :
  1. Operasi penjumlahan (+) dan pengurangan (-) sama kuat, artinya operasi yang terletak di sebelah kiri dikerjakan terlebih dahulu.
  2. Operasi perkalian (x) dan pembagian (:) sama kuat, artinya operasi yang terletak disebelah kiri dikerjakan terlebih dahulu.
  3. Operasi perkalian (x) dan pembagian (:) lebih kuat dari pada operasi penjumlahan (+) dan pengurangan (-), artinya operasi perkalian (x) dan pembagian (:) dikerjakan terlebih dahulu dari pada operasi operasi penjumlahan (+) dan pengurangan (-).
Aturan tersebut juga berlaku pada operasi hitung campuran pada bilangan pecahan.
Contoh :
Sederhanakan bentuk 45/9 – 12/3 + 31/6 !
Penyelesaian :
45/9 – 12/3 + 31/6  = (4 - i + 3) + (5/9 - 2/3 + 1/6)
45/9 – 12/3 + 31/6  = six + (10/18 - 12/18 + 3/18)
45/9 – 12/3 + 31/6  = six +1/18
45/9 – 12/3 + 31/6  = 61/18

6. Operasi Hitung pada Pecahan Desimal 

a. Penjumlahan dan pengurangan pecahan desimal

Penjumlahan dan pengurangan pecahan desimal dilakukan pada masing-masing nilai tempat dengan cara bersusun. Urutkan angka - angka ratusan, puluhan, satuan, persepuluhan, perseratusan, dan seterusnya dalam satu kolom.
Contoh :
Hitunglah hasil operasi  hitung berikut :
  • 28,62 + 2,27
  • 54,36 - 36,68
Penyelesaian :
  • 26,62
      2,27 +
    30,89
  • 54,36
    36,68-
    17,68

b. Perkalian pecahan desimal

Untuk menentukan hasil perkalian bilangan desimal, perhatikan contoh berikut :
Hitung hasil perkalian berikut !
  • 1,52 x 7,6
  • 0,752 x 4,32
Penyelesaian :
  • 1,52 x 7,6 = 152/100 x 76/10 = 152 x 76 / 1.000 = 11.552/1.000 = 11.552
  • 0,752 x 4,32 = 752/1.000 x 432/100 = (752 x 432)/100.000 = 324.864/100.000 = 3,24864
Nah segini dulu ya artikel kali ini. Mohon maaf apabila ada kesalahan. Baca juga lanjutan dari artike ini yaitu tentang pembulatan dan bentuk baku pecahan
Akhir kata wassalamualaikum wr. wb.
Materi ini dikutip dari buku matematika konsep dan aplikasinya karangan Dewi Nuharini dan Tri Wahyuni.
Subscribe to: Posts (Atom)