Home Posts filed under Search results for cara-membuat-dan-menyajikan-tabel
Showing posts sorted by date for query cara-membuat-dan-menyajikan-tabel. Sort by relevance Show all posts
Showing posts sorted by date for query cara-membuat-dan-menyajikan-tabel. Sort by relevance Show all posts

Cara Mengumpulkan Information Dalam Ilmu Statistik

How are u guys ?????
I promise u fine, right!!!!
Heheheheh :D
Nah guys kali ini gw punya artikel beberapa cara pengumpulann information nih :       

1. Penelitian langsung di lapangan atau laboratorium.
     Penelitian di lapangan biasanya disebut dengan observasi atau pengamatan merupakan teknik pengumpulan information dengan cara pengamatan terhadap objek, baik secara langsung maupun tidak langsung, misalnya penelitian terhadap situs-situs purbakala dan penelitian di dalam laboraturium. Pengamatan dapat dilakukan dengan :
  1. Pengamatan langsung, yaitu pengamatan yang dilakukan tanpa perantara (secara langsung) terhadap objek yang diteliti.
  2. Pengamatan tak langsung, yaitu pengamatan yang dilakukan terhadap objek melalui perantara suatu alat atau cara.
  3. Pengamatan partisipasif, yaitu pengamatan yang dilakukan dengan cara ikut ambil bagian atau melibatkan diri dalam situasi yang dialami oleh responden. Cara ini banyak dilakukan terutama dalam penelitian psikologi, sosiologi, maupun antropologi.
2.Interview (wawancara)
     Teknik pengumpulan information yang dilakukan dengan cara mengadakan tanya jawab, baik secara langsung maupun tidak langsung dengan responden. Pada wawancara langsung, peneliti mengadakan tatap muka langsung dengan responden, sedangkan pada wawancara tidak langsung, peneliti mewawancarai perantara tahu persis tentang objek yang diteliti.

 3.Kuesioner (Angket)
     Angket dapat dipandang sebagai teknik pengumpulan information yang banyak kesamaannya dengan wawancara. Perbedaannya adalah wawancara dilakukan secara lisan, sedangkat angket dilakukan secara tertulis. Bentuk penyusunan angket ada dua macam, yaitu :

  1.  Angket berstruktur, yaitu angket yang menyediakan kemunkinan jawaban.
  2.  Angket tak berstruktur, yaitu angket yang tidak menyediakan kemungkinan jawaban.
                                                  contoh angket :


Nah segini dulu yah guys materi dari gw
Untuk menambah pemahaman baca juga artikel tentang :
Assalamualaikum Bye bye………………………..

Cara Menyajikan Tabel Distribusi Frekuensi Information Kelompok

Hallo guys.......!!!
Kli ini gw punya artikel tentang gimana caranya nyajiin tabel distribusi frekuensi information kelompok.
Simak ya!!!!!

Data yang telah dikumpulkan, baik dari populasi maupun sampel untuk keperluan laporan dan atau analisis selanjutnya, perlu diatur, disusun, dan disajikan dalam bentuk yang jelas dan baik. Secara garis besar penyajian information dibagi menjadi dua cara yaitu dalam bentuk tabel dan grafik.

Dalam menyajikan tabel information klompok itu kadang beberapa bagian orang merasa kesulitan karena mereka berfikir untuk menyusun satu persatu dahulu dari banyak datang yang mereka dapatkan.
Padaha jika mereka tau ilmunya mereka tidak akan kebingungan seperti itu. Maka dari saya akan berbagi ilmunya.

Nah berikut cara meyajikan tabel distribusi frekuensi information kelompok :
1. Langkah yang pertama kita surfey nilai lxxx siswa :
    Data Untuk lxxx siswa :
    lxxx 80 lxx 68 xc 92 lxxx lxx 63 76
    49 84 71 72 35 93 91 74 lx 63
    48 xc 92 85 83 76 61 99 83 88
    74 lxx 38 51 73 71 72 95 82 70
    81 91 56 65 74 xc 97 lxxx lx 66
    98 93 81 93 43 72 91 59 67 88
    87 82 74 83 86 67 88 71 89 79
    82 78 73 86 68 75 81 77 63 75

2. Tentukan rentangan (R) !
     Rentangan (R) = Nilai terbesar - Nilai terkecil
                  R  = 99 - 35
                       = 64

3. Tentukan Banyaknya kelas untuk interval tabel!
Banyaknya Kelas (k) = 1 + 3,3 log n
                                    k  = 1 + 3,3 log 80
                                         = one  + (3,3) (1,9031)
                                         = 7,2802
ket : n = banyaknya data
Maka kita dapat membuat daftar dengan banyaknya kelas seven atau 8

4. Tentukan panjang kelas interval !
     P = R/k
        = 64/7
        = 9,14
Maka panjang kelas dapat kita ambil nine atau 10

5. Tentukan batas bawah kelas interval pertama !
Batas bawah interval kelas pertama dapat diambil dari information yang terkecil atau information yang lebih kecil dari information terkecil tetapi selisihnya kurang dari panjang kelas dan kelas pertama tidak boleh
mempunyai frekuensi sama dengan nol.
maka saya ambil saja batas bwah interval pertamanya adalah 31

6. Amati berapa banyak angka yang sama (turus) pada setiap kelas dan tulis pada kolom turus dengan tanda (I)

7. Isi jumlah frekuensi sesuai banyaknya turus.
Maka akan di peroleh tabel distribusi frekuensi sebagai berikut :

nah guys sambil coba yah bikin sendiri
Segini dulu yah materi dari saya ntar klo panjang-panjang malah bikin bingung lagi
Asslamualaikum farewell bye.....

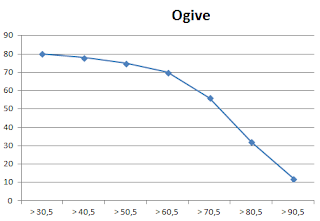
Cara Membuat Dan Menyajikan Tabel Distribusi Relatif Dan Kumulatif Beserta Ogiv, Histogram, Dan Poligon Frekuensinya.

Apa kabar guys???

kli ini gw punya ilmu tentang cara membuat tabel distribusi relatif dan kumulatif.
Simak ya!!!!!

Jika banyaknya frekuensi pada tiap interval dibandingkan denga jumlah information keseluruhan dan dinyatakan dalam bentuk persen, maka akan didapat frekuensi relatif (f rel.).
Contoh tabel distribusi frekuensi :

Rumus : f rel-... = (frekuensi ke...(f-..)/jumlah seluruh data(n))x100%
Dari tabel di atas frekuensi relatif interval pertamanya adalah
f rel-1 = (2/80)x100% = 2,5%
dan untuk yang ke dua dan seterusnya dengan cara yang sama juga :
f rel-2 = (3/80)  x100% =   3,75%
f rel-3 = (5/80)  x100% =   6,25%
f rel-4 = (14/80)x100% = 17,50%
f rel-5 = (24/80)x100% = 30.00%
f rel-6 = (20/80)x100% = 25,00%
f rel-7 = (12/80)x100% = 15,00%

Maka kita masukan f rel ke tabel :

Kemudian kita buat tabel frekuensi kumulatifnya.
Ada dua frekuensi kumulatif :
1. Frekuensi kumulatif kurang dari adalah frekuensi yang diperoleh dari jumlah frekuensi yang kurang dari atau sama dengan tepi atas kelas yang bersangkutan.
Tabel frekuensi kumulatif kurang dari :



kemudian kita membuat grafik dari frekuensi kumulatif kurang dari tersebut ( Ogive ).



2. Frekuensi kumulatif lebih dari adalah diperoleh dari jumlah frekuensi yang lebih atau sama dengan tepi bawah kelas yang bersangkutan.
Tabel frekuensi kumulatif lebih dari :
Ogive frekuensi kumulatif lebih dari :


Catatan ; ingat setiap grafik yang menunjukan frekuensi kumulatif di sebut Ogive

Nah sampe sini dulu yah meteri dari gw
Untuk menambah pemahaman baca juga artikel tentang :
Asalamualaikum farewell bye.....

Macam - Macam Diagram Dalam Ilmu Statistik

Nih guys macam - macam diagram :

1. Diagram Garis
 Untuk menggambarkan keadaan yang berkesinambungan atau kontinu maka dengan cara membuat diagram garis
Contoh :

2. Diagram Batang
Seperti halnya pada diagram garis, untuk information yang variablenya berbentuk kategori atau atribut (mempunyai ciri-ciri khusu) dapat disajikan dalam bentuk diagram batang.
Contoh :

3, Diagram lingkaran
Pada penyajian information dalam betuk diagram lingkaran, lingkaran di bagi dalam bentuk juring-juring lingkarang sesuai dengan information yang bersangkutan. Luas masing-masing juring sebanding dengan prosentase information yang bersangkutan

Contog :


4. Piktogram
Piktogram ialah diagram berbentuk gambar. Setiap gambar digunakan sebagai satua. Misalya i orang mewakili M jiwa.
contoh :

5. Histogram
Histogram merupakan diagram  untuk menyajika information dalam bentuk distribusi frekuensi. Sumbu tegak untuk menyatakan frekuensi dan sumbu mendatar untuk menyatakan batas interval kelas.
Contoh :


Nah guys sekian dulu yah materi dari gw 
Untuk menambah pemahaman baca juga artikel tentang :
asalamualaikum farewell bye....

Rumus Rata-Rata (Mean), Median, Dan Modus Information Tunggal (Statistik)

Nih guys gw punya ilmu tentang bagaimana caranya menghitung Rata-Rata, Median, dan Modus information tunggal.
Simak yah guys !!!!!
1. Rumus Rata-Rata Data tunggal 
Dalam kehidupan sehari-hari, rata-rata lebih banyak dikenal, misalnya rata-rata gaji pegawai suatu perusahaan tiap bulan.
Nilai rata-rata yang akan dibahas dalam artikel ini meliputi rata-rata hitung, rata-rata ukur ( Rata-Rata Geometrik ), dan rata-rata harmonik.
a. Rumus Rata-Rata hitung information tunggal
Dari sekumpulan information X1,X2,X3,...,,Xn, maka rata-rata hitung dari information tersebut adalah :
       
keterangan : n = Banyak data
contoh :
tentukan nilai rata-rata hitung dari information 6,4,8,10,11,10,7

Jawab :
b. Rumus Rata-Rata Ukur ( Rata-Rata Geometrik)
Jika perbandingan tiap dua information berurutan tetap atau hampir tetap, rata-rata ukur lebih baik digunakan dari pada rata-rata hitung, apabila kehendaki rata-ratanya.
Rumus :

Contoh ; 
Hitunglah rata-rata ukur information berikut : 2,4,8,16!
Jawab :
 
c. Rata-Rata Harmonik
       Rumus :

Contoh :
Hitunglah rata-rata Harmonik dari information berikut : 3,5,6,6,7,10,12!
Jawab :



2. Rumus Modus Data Tunggal (Mo)
Modus dari suatu information adalah information yang sering muncul atau information yang mempunyai frekuensi tertinggi.
Contoh :
Tentukan Modus information berikut : 3,4,4,5,5,5,6,7
Jawab :
Modus information tersebut adalah 5

3. Rumus Median Data tunggal
Median (Me) adalah nilai pertengahan dari sekelompok information yang telah diurutkan menurut besarnya.
Rumus :
   a. Jika banyak information ganjil :
Contoh :
Tentukan median dari information :
3,7,6,4,5
Jawab :
maka kita urutkan terlebih dulu datanya menjadi 3,4,5,6,7
maka mediannya : information ke ; (n+1)/2 = (5+1)/2 = 3
Maka information ke-3 adalah 5

     b. Jika bayak datanya genap :


Contoh :
Tentukan median dari information ;
1,2,4,3
Jawab ;
Maka kita urutkan dahulu datnya :
Data ke-(n/2)+  data ke-((n/2)+1)/2 = information ke-(4/2)+data ke((4/2)+1/2
                                                         =(data ke-2 + Data ke-3)/2
                                                         =       (2 + 3)/2
                                                         = 2,5


Nah segini dulu yah materinya
Untuk menambah pemahaman baca juga artikel tentang :

Ukuran Penyebaran Information (Dispersi)

how r u guys?
Kali ini gw bakalan kasih kalian ilmu tentang penyebaran data.
Simak ya !

Ada beberapa ukuran penyebaran information (dispersi), antara lain

1. Jangkauan/Range (R)
     Ukuran penyebaran information yang paling mudah adalah range. Apabila sekumpulan information sudah tersusun dari yang terkecil hingga yang terbesar, maka make dari information adalah selisih information terbesar (X-max) dengan information terkecil (X-min)
Maka diperoleh rumus :
                                       R = (X-max - X-min)
Contoh :
Tentukan make dari information 20,30,35,40,50,56,60 !
Jawab :
X-max = 60
X-min = 20

R = (X-max - X-min)
    = lx - 20
    = 40

Maka rangenya adalah 40

2. Rata-Rata Simpangan (RS)














3. Simpangan Baku (Deviasi Standar)
Barangkali ukuran simpangan baku yang paling banyak digunakan adalah simpangan baku atau deviasi setandar, karena mempunyai sifat-sifat matematik (mathematical property) yang sangat penting dan berguna untuk pembahasan teoty dan analisis statistik selanjutnya.
















4. Kuartil (Q)
 a. kuartil information tunggal
   Langkah-langkah yang tempuh untuk mencari kuartil :
     - Susunan information menurut ururannta
     - Tentukan letak Kuartil
     - Tentukan nilai kuartilnya
    Rumus letak kuartil ke-i :




contoh:
Tentukan nilai quarti dari information berikut ini :
1,6,9,3,5,8,10

Jawab :
kita urutkan information terlebih dahulu menjadi 1,3,5,6,8,9,10






 b. Kuartil information berkelompok
Rumus :











Contoh :
Tentukan Q1 dari tabil di bawah :
Jawab :
Untuk Q1, maka i = 1
n = Jumlah seluruh frekuensi = 80
Letak Q1 = (1/4)n = (1/4)80 = 20
sehingga letak Q1 pada interval ke-3, yaitu xl - 44, maka :
Tb1 = xl - 0,5 = 39,5
f1    = 13
F1   = 8 + 10 = 18
c     = 35 - xxx = 5





c. Jangkauan Kuartil.dan Simpangan kuartil
Dari sekumpulan information yang mempunyai kuartil bawah Q1 dan kuartil atas Q3, Jangkauan kuartil dan simpangan kuartil adalah sebagai berikut :
Untuk contoh bisa kalian cari sendiri soalnya mudah ko

5. Desil (D)
a.Desil Data Tunggal
Kumpulan information yang di bagi 10 bagian yang sama, maka diperoleh sembilan pembagi dan tiap pembagi dinamakan desil.
Cara untuk menentukan desil :
    - Susunlah information menurut urutan nilainya
    - Tentukan letak desilnya
    - Hitung nilai desilnya
Letak desil ke-i dapat di tentukan dengan rumus :
Lokasi Di = information ke-(i(n + 1) / 10)










6. Persentil (P)
kumpulan information yang dibagi menjadi 100 bagian yang sama, maka di peroleh 99 pembagi dan tiap pembagi dinamakan persentil.
cara untuk mendapatkan persentil :
a. susunlah information menurut urutan nialinya
b. Tentukan letak persentilnya
c. Hitung nilai persentilnya

Letak persentil ke-i dapat di tentunkan dengan rumus berikut :

 Rumus presentil untuk information kelompok :











7. Angka Baku
Angka baku digunakan untuk mengetahui perbedaan suatu kejadian dibanding dengan kebiasaannya. Semakin besar angka bakunya semakin baik nilai tersebut dibandingkan dengan nilai yang lain yang memiliki angka baku lebih kecil.
Rumus :










Contoh :
diketahui : information : 2,7,8,10,4,dan5
                   rata-rata hitung : 6
                   Simpangan baku : akar 7
Tentukan angka baku dari 2!
jawab :












8. Koefisien Variansi (KV)
Koefisien variansi adalah perbandingan antara simpangan baku dengan rata-rata suatu information dan dinyatakan dalam%
Rumus :










Contoh :
lampu neon rata-rata dapat dipakai selama 2.800 jam dengan simpangan baku 700 jam, sedangkan lampu pijar dapat dipakai rata-rata selama 3.500 jam dengan simpangan  baku 1.050 jam. dara information di atas manakah yang lebih baik.
Jawab :








dari perhitungan koefisien variansi, lampu neon lebih baik dari lampu pijar, karena KV neon < KV lampu pijar


Nah segini yh materi dari saya
Untuk menambah pemahaman baca juga artikel tentang :
asalamualaikum goodbye bye.......
Subscribe to: Posts (Atom)