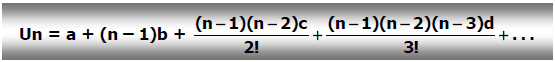Hallo temen-temen???
Pertama-tama gue ucapin trimakasih buat para pengunjung spider web log gue :). Slamat datang di spider web log paling bermanfaat sedunia.
Dan gue doaian semoga orang-orang yang ngunjungin spider web log gue pada masuk surga semua, trs selama hidupnya selalu di beri kemudahan, trs all the best deh buat kalian :D
Udah kaya ulang tahun aja ya ???.... Sorry ya klo penulis suka bercanda :)
Kembali lagi bersama gue muhamad pajar sidik, gue adalah seorang penulis blogger yang ganteng dan baik hati :D cieeee.....
Di hari yang indah ini alhamdulillah gue bisa nulis artikel kembali, yang mudah-mudahan artikel ini bisa bermanfaat buat kalian semua.
Kali ini gue bakalan nulis artikel tentang Rumus Barisan Aritmatika Bertingkat Banyak, Tanpa panjang lebar lagi yo cheque it out !
Pertama-tama gue ucapin trimakasih buat para pengunjung spider web log gue :). Slamat datang di spider web log paling bermanfaat sedunia.
Dan gue doaian semoga orang-orang yang ngunjungin spider web log gue pada masuk surga semua, trs selama hidupnya selalu di beri kemudahan, trs all the best deh buat kalian :D
Udah kaya ulang tahun aja ya ???.... Sorry ya klo penulis suka bercanda :)
Kembali lagi bersama gue muhamad pajar sidik, gue adalah seorang penulis blogger yang ganteng dan baik hati :D cieeee.....
Di hari yang indah ini alhamdulillah gue bisa nulis artikel kembali, yang mudah-mudahan artikel ini bisa bermanfaat buat kalian semua.
Kali ini gue bakalan nulis artikel tentang Rumus Barisan Aritmatika Bertingkat Banyak, Tanpa panjang lebar lagi yo cheque it out !
Ada yang unik dalam pembelajaran barisan aritmatika. Dalam barisan aritmatika mungkin jika beda tiap sukunya sama kita akan mudah menentukannya dengan rumus suku ke-n aritmatika. Namun bagaimana jika beda tiap sukunya juga beda??? Nah masalah ini akan saya bahasa kepada teman-teman semua. Permasalahan seperti ini sering sekali keluar dalam berbagai macam tes. Bisa keluar di tes psikotes kerja, psikotes kuliah, bahkan dalam SBMPTN pun sangat sering keluar. Dalam United Nations pun sering keluar. Nama permasalahanya adalah tentang Barisan Aritmatika Bertingkat Banyak.
Pengertian Barisan Aritmatika Tingkat Banyak
Barisan aritmatika tingkat banyak adalah "kumpulan suku-suku pada barisan aritmatika yang memiliki beda suku yang bertingkat". Jadi pada barisan artimatika bertingkat banyak ini beda tiap sukunya tidak sama atau bedanya bertingkat sampai beda pada tingkatan akhirnya sama. Misalkan :
Karena beda tiap suku tidak sama maka akan menghasilkan suatu tingkatan-tingkatan tertentu sampai beda pada tingkat suku terakhirnya sama.
Rumus Barisan Aritmatika Bertingkat Banyak
Dengan menggunakan pembuktian Binomuim Newton (tidak dijelaskan di sini), maka rumus umum suku ke-n barisan aritmatika bertingkat banyak adaalah :
Keterangan :
a = Suku ke-1 Barisan mula-mula
b = Suku ke-1 Barisan tingkat satu
c = Suku ke-1 Barisan tingkat dua
d = Suku ke-1 Barisan tingkat tiga
dan seterusnya....
- Rumus Barisan aritmatika tingkat 1 jika c = d = .... = 0, sehingga diperoleh :
Un = a + ( n - i )b Sudah di bahas pada artikel rumus suku ke-n barisan aritmatika. - Rumus Barisan aritmatika tingkat 2 jika d = e = ... = 0, sehingga diperoleh :
Un = a + ( n - i )b + (( n - i )( n - two ).c)/2 - Rumus Barisan aritmatika tingkat 3 jika e = f = ... = 0, sehingga diperoleh :
Un = a + ( n - i )b + ((( n - i )( n - two ).c)/2) + ((( n - i )( n - two )( n - three ).d)/6) - dan seterusnya....
Contoh Soal Barisan Aritmatika Bertingkat Banyak
Tentukan suku ke-6 dari barisan aritmatika bertingkat 5, 6, 9, 14,..,...
Jawab :
Pertama kita tentukan berapa tingkat barisan 5, 6, 9, 14,...,...
Ternyata ada two tingkat barisan pada barisan 5, 6, 9, 14, ..., ...
Maka :
a = 5
b = 1
c = 2
U6 = .... ?????
Kemudian kita masukan ke dalam Rumus barisan aritmatika tingkat 2 :
Un = a + ( n - i )b + (( n - i )( n - two ).c)/2
U6 = five + ( half dozen - i )1 + (( half dozen - i )( half dozen - two ).2)/2
U6 = five + five + ( five x four x 2)/2
U6 = 10 + 40/2
U6 = 10 + 20
U6 = 30
Jadi suku ke-6 dari barisan aritmatika bertingkat 5, 6, 9, 14, ..., ... adalah 30
Kesimpulan
Jadi untuk barisan aritmatika bertingkat memiliki rumus tersendiri, yang artinya tidak bisa diselesaikan dengan rumus Un = a + ( n - i )b. tapi harus menggunakan rumus barisan aritmatika bertingkat yang sudah saya berikan di atas tadi.
Nahh segini dulu ya artikel kali ini, mohon maaf apabila ada salah-salah kata
Untuk menambah pengetahuan baca juga artikel tentang :
Untuk menambah pengetahuan baca juga artikel tentang :
Akhir kata wassalamualaikum wr. wb.