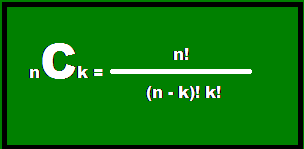Rumus Kombinasi Peluang

Hallo temen-temen???

Pertama-tama gue ucapin trimakasih buat para pengunjung weblog gue :). Slamat datang di weblog paling bermanfaat sedunia.

Dan gue doaian semoga orang-orang yang ngunjungin weblog gue pada masuk surga semua, trs selama hidupnya selalu di beri kemudahan, trs all the best deh buat kalian :D

Udah kaya ulang tahun aja ya ???.... Sorry ya klo penulis suka bercanda :)

Kembali lagi bersama gue muhamad pajar sidik, gue adalah seorang penulis blogger yang ganteng dan baik hati :D cieeee.....

Di hari yang indah ini alhamdulillah gue bisa nulis artikel kembali, yang mudah-mudahan artikel ini bisa bermanfaat buat kalian semua.

Kali ini gue bakalan nulis artikel tentang Rumus Kombinasi Peluang , Tanpa panjang lebar lagi yo banking concern gibe it out !

Pernahkah anda mengikuti atau melihat sebuah kuis undian yang mengundi dengan cara menggunakan bola berwarna - warni ??? Dalam kuis tersebut biasanya orang yang bermain dalam kuis memilih satu bola atau beberapa bola dengan warna tertentu dari sekian banyak warna. Ktika orang itu berhasil mengambil bola sesuai dengan apa yang diperintahkan pemandu kuis, maka orang itulah yang menjadi pemenangnya. Namun permainan kuis seperti ini ternyata ada pula dalam ilmu matematika, ilmu tersebut adalah tentang peluang. Namun ada sub materi spesifik yang membahas tentang permainan-permainan seperti itu, yaitu materi "Kombinasi".

Pengertian Kombinasi 

Dalam ilmu matematika peluang, kombinasi adalah "penggabungan objek-objek tanpa memperhatikan urutan tertentu". Jadi kombinasi itu menggabungkan objek-objek namun tanpa memperhatikan urutan, contoh :

kita memiliki tiga objek yaitu objek "a", objek "b", dan objek "c". Nah apabila kita kombinasikan maka menjadi :

abc

Hasil kombinasinya adalah hanya satu yaitu abc. Walaupun masih bisa abc, cba, bca, dan seterusnya, namun dalam kombinasi hanya dihitung satu saja, karena kombinasi tidak memperhitungkan sebuah urutan.

Rumus Kombinasi Peluang

Keterangan :

C =  Kombinasi atau Combinasi

n  = Jumlah banyaknya objek

k  =Jumlah banyaknya objek yang diperintahkan

Contoh soal :

Dari suatu kotak terdapat xx bola dimana eight warnanya merah, vii warnanya putih, dan sisanya berwarna hitam. Jika diambil ii bola dari kotak tersebut, berapakah banyak cara untuk medapatkan dua warna  merah ?

Jawab :

Dik :

n = 8

k = 2

Dit :

Banyak cara pengambilan dua bola warna merah ???

Maka :

Jadi banyak cara untuk mengambil dua bola berwarna merah adalah 28 cara.

Kesimpulan

Jadi intinya kombinasi itu tidak memperdulikan sebuah urutan, beda dengan permutasi yang mementingkan sebuah urutan contoh :

Dalam permutasi untuk menyusun A, B, dan C ada beberapa cara yaitu :

ABC, BCA, CAB, dan seterusnya

Nah dalam combinasi objek A, B, dan C apabila disusun dengan cara kombinasi hanya akan ada satu cara yaitu ABC saja, karena BCA dengan ABC atau seterusnya itu hanya membolak - balik susunan saja. Jadi dalam kombinasi yang di hitung hanyalah satu yaitu ABC.

Nah segini dulu ya artikel kali ini. Baca juga artikel tentang:

• Rumus Permutasi Peluang
• Rumus Frekuensi Harapan
• Rumus Peluang Suatu kejadian
• Rumus Komplemen Peluang 
• Rumus Peluang Kejadian Majemuk  
• Rumus Peluang Kejadian Bersyarat

mohon maaf apabila ada salah salah kata.

Akhir kata wassalamualaikum wr. wb.

Rumus Peluang Suatu Kejadian

Hallo temen-temen???
Pertama-tama gue ucapin trimakasih buat para pengunjung weblog gue :). Slamat datang di weblog paling bermanfaat sedunia.
Dan gue doaian semoga orang-orang yang ngunjungin weblog gue pada masuk surga semua, trs selama hidupnya selalu di beri kemudahan, trs all the best deh buat kalian :D
Udah kaya ulang tahun aja ya ???.... Sorry ya klo penulis suka bercanda :)
Kembali lagi bersama gue muhamad pajar sidik, gue adalah seorang penulis blogger yang ganteng dan baik hati :D cieeee.....
Di hari yang indah ini alhamdulillah gue bisa nulis artikel kembali, yang mudah-mudahan artikel ini bisa bermanfaat buat kalian semua.
Kali ini gue bakalan nulis artikel tentang Rumus Peluang Suatu Kejadian , Tanpa panjang lebar lagi yo banking venture gibe it out !

Melempar koin adalah suatu kebiasaan yang dilakukan dalam menentukan siapa yang lebih dahulu, siapa yang menempati posisi tertentu, atau yang lainnya dalam sebuah pertandingan atau permainan. Hal tersebut dilakukan karena koin memiliki dua sisi dengan gambar yang berbeda sehingga memungkinkan untuk dipakai dalam penentuan suatu kejadian. Hal seperti itu pun termasuk dalam ilmu matematika yaitu tentang peluang suatu kejadian. Kali ini saya akan membahas tentang rumus peluang suatu kejadian.

Pengertian Peluang Suatu Kejadian

Peluang adalah "suatu kemungkinan yang akan terjadi pada sebuah peristiwa". Peluang suatu kejadian bisa dihitung dengan matematika yang biasa kita sebut dengan prediksi. Namun beda dengan cara memprediksi seorang peramal, klo seorang peramal mereka menggunakan ilmu spiritual untuk memprediksikan suatu hal. Nah klo dalam ilmu matematika, kita memprediksi suatu hal berdasarkan logika atau berdasarkan ilmu yang nyata (exak).  

Rumus Peluang Suatu Kejadian

Keterangan :

P : Peluang Suatu kejadian

Influenza A virus subtype H5N1 : Kejadian Influenza A virus subtype H5N1 (hanya simbol sebuah kejadian)

n : Banyaknya suatu kejadian

due south : Seluruh Kejadian

Jadi maksud rumus di atas adalah, peluang suatu kejadian dilambangkan dengan "P" diamana hanya diambil huruf depan dari kata "Peluang". Untuk suatu kejadian kita lambangkan dengan "A" saja, tujuannya untuk mempermudah saja. Dan untuk lambang "n" adalah lambang yang menunjukalan banyaknya nilai suatu kejadian, lambang tersebut di ambil dari huruf depan kata "nilai". Jadi untuk simbol banyaknya nilai seluruh kejadian diberi simbol "n(S)" dan banyaknya nilai suatu kejadian dilambangkan dengan "n(A)".

Kita masuk ke contoh soal,

Contoh :

Pada pelemparan sebuah dadu, tentukanlah peluang kejadian munculnya bilangan genap!!!!!

Jawab :

Untuk menyelesaikan soal seperti ini pertama kita cari dahulu jumlah bilangan genap yang ada pada sebuh dadu. Ternyata dalam sebuah dadu ada iii bilangan genap yaitu 2, 4, dan 6, maka :

Influenza A virus subtype H5N1 = {2, 4, 6}

n(A) = 3

Kemudian cari banyaknya semua bilangan yang ada pada dadu, ternyata pada sebuah dadu ada bilangan 1, 2, 3, 4, 5, dan 6. Maka :

due south = {1, 2, 3, 4, five ,6)

n(S) = 6

Kemudian setelah kita menemukan n(A) dan n(S), kita masukan n(A) dan n(S) ke dalam rumus peluang suatu kejadian, mejadi :

P(A) = n(A) / n(S)

P(A) = 3/6

P(A) = 1/2

Jadi peluang dari munculnya bilangan genap pada satu kali pelemparan sebuah dadu adalah 1/2 atau 50%.

Kesimpulan :

Jadi untuk menentukan sebuah peluang suatu kejadian itu kita harus mengetahui nilai banyaknya suatu kejadian dan banyaknya seluruh kejadian. kemudian baru kita selesaikan dengan menggunakan rumus P(A) = n(A) / n(S)

Nah segini dulu ya artikel kali ini. Mohon maaf apabila ada salah salah kata.
Untuk menambah pengetahuan baca juga artikel tentang :

• Rumus Frekuensi Harapan
• Rumus Permutasi Peluang
• Rumus Kombinasi Peluang
• Rumus Komplemen Peluang
• Rumus Peluang Kejadian Majemuk
• Rumus Peluang Kejadian Bersyarat 

Akhir kata wassalamualaikum wr. wb.

Rumus Frekuensi Harapan

Hallo temen-temen???

Pertama-tama gue ucapin trimakasih buat para pengunjung spider web log gue :). Slamat datang di spider web log paling bermanfaat sedunia.

Dan gue doaian semoga orang-orang yang ngunjungin spider web log gue pada masuk surga semua, trs selama hidupnya selalu di beri kemudahan, trs all the best deh buat kalian :D

Udah kaya ulang tahun aja ya ???.... Sorry ya klo penulis suka bercanda :)

Kembali lagi bersama gue muhamad pajar sidik, gue adalah seorang penulis blogger yang ganteng dan baik hati :D cieeee.....

Di hari yang indah ini alhamdulillah gue bisa nulis artikel kembali, yang mudah-mudahan artikel ini bisa bermanfaat buat kalian semua.

Kali ini gue bakalan nulis artikel tentang Rumus Frekuensi Harapan, Tanpa panjang lebar lagi yo banking concern jibe it out !

Uang Logam Rp.1.000,00 Indonesia

Uang adalah suatu alat untuk melakukan sebuah transaksi. Namun uang logam seperti gambar di atas tidak hanya di gunakan untuk transaksi, akan tetapi bisa digunakan untuk permainan-permainan, seperti permainan sulap, permaianan menebak gambar uang, dan yang lainnya. Ternyta pada permainan-permaian tersebut ada kaitannya dengan ilmu matematika. Ilmu peluang ialah ilmu yang sangat menyenangkan yang membahas akan permaiana-permainan seperti principal dadu, principal koin, dan lain sebagainya. Peluang adalah materi yang sangat dekat sekali dengan kehudupan yang kita jalani sehari-hari, contohnya dengan peluang kita bisa antisipasi atau memperkirakan sesuatu yang akan terjadi dengan logis. BMKG memperkirakan sebuah cuaca di daerah tertentu tentunya dengan menggunakan ilmu peluang juga yang kemudian dikaitkan dengan tanda tanda tertentu. Seorang pelaut tentunya memprediksikan dahulu akan perjalanannya sebelum ia pergi berlayar, seorang siswa ktika akan menghadapi ulangan diapun memprediksi kan soal apa yang akan keluar. Namun ingatlah jika kita ingin memprediksi sesuatu dengan logika atau logis, gunakan lah selalu ilmu peluang, jangan pernah menggunakan feeling apalagi percaya akan hal yang mistis. Kali ini saya akan berbagi submateri peluang yaitu tentang Rumus Frekuensi Harapan. Rumus frekuensi harapan ini merupakan lanjutan dari materi peluang suatu kejadian, Maka dari itu saya sarankan jika anda belum membaca artikel atau materi tentang peluang suatu kejadian maka baca dahulu artikelnya di link Rumus Peluang Suatu Kejadian. 

Pengertian Frekuensi Harapan

Frekuensi harapan adalah "banyaknya suatu percobaan dikalikan dengan peluang suatu kejadian". Jadi pada frekuensi harapan ini kita akan menghitung berpa peluang suatu kejadian dengan berkali kali percobaan, atau bisa kita sebut juga sebagai melakukan experiment. Frekuensi harapan ini bisa kalian praktekan secara langsung, misalnya kalian melempar uang logam Rp.1.000,00 sebanyak 100 kali, kemudian kalian hitung berapa banyak sisi gambar nominal uang dan berapa banyak sisi gambar angklung selama seratus kali pelemparan tersebut, nah setelah kalian melakukan hal tersebut maka kalian akan mengetahui berapakah frekuensi harapan untuk kedua sisi pada uang logam Rp.1.000,00. 

Rumus Frekuensi Harapan

Keterangan :

Fh : Frekuensi harapan

P : Peluang

Influenza A virus subtype H5N1 : Kejadian Influenza A virus subtype H5N1 (hanya lambang suatu kejadian)

n : Banyaknya suatu percobaan

Dari rumus di atas ada "Fh" adalah sebuah simbol dari Frekuensi harapan yang di ambil dari kata depan "Frekuensi dan harapan". Lambang "P" adalah sebuah simbol yang melambangkan peluang suatu kejadian, logo "P" tersebut diambil dari hurup depan kata "Peluang". Lambang "A" adalah sebuah simbol yang mewakili akan suatu kejadian, lambang "A" tersebut hanya untuk mempermudah saja. Dan Lambang "n" adalah simbol yang melambangkan banyaknya suatu percobaan yang dilakukan, lambang "n" ini dipilih karena lamban "n" merupakan lambang yang sudah umum dalam menentukan sebuah banyak atau nilai tertentu.

Perlu di ingat bahwa :

P(A) = n(A)/n(S)

Contoh soal :

Tiga buah uang logam yang berisi gambar (G) dan angka (A) dilempar bersama-sama sebanyak lxxx kali. tentukan harapan munculnya tiga-tiganya angka!!!

Jawab :

Untuk menyusun soal seperti ini pertama kita hitung dulu banyaknya seluruh nilai kejadian, seluruh kejadian kita lambangkan dengan S, maka :

southward = {GGG, GGA, GAG, AGG, AAG, AGA, GAA, GGG}

n(S) = 8

Dan untuk yang muncul tiga-tiganya Influenza A virus subtype H5N1 hanyala satu yaitu {AAA}. maka :

Influenza A virus subtype H5N1 = {AAA}

n(A) = 1

Dan banyaknya percobaan adalah sebanyak lxxx kali maka :

n = 80

Maka :

Fh = P(A) x n

Fh = ( n(A)/n(S) ) x n

Fh = (1/8) x 80

Fh =  10

Jadi harapan munculnya tiga-tiganya angka adalah sebanyak 10 kali.

Kesimpulan

Jadi frekuensi harapan itu adalah suatu frekuensi atau jumlah banyaknya percobaan dikalikan dengan peluang suatu kejadian sehingga menghasilkan banyaknya harapan muncul suatu kejadian tertentu.

Nah segini dulu ya artikel kali ini, mohon maaf apabila ada kesalahan
Untuk menambah pemahaman baca juga artikel tentang :

• Rumus Peluang Suatu Kejadian 
• Rumus Komplemen Peluang
• Rumus Peluang Kejadian Majemuk
• Rumus Permutasi Peluang
• Rumus Kombinasi Peluang 
• Rumus Peluang Kejadian Bersyarat

Akhir kata wassalaumualaikum wr. wb.

Rumus Permutasi Peluang

Hallo temen-temen???
Pertama-tama gue ucapin trimakasih buat para pengunjung weblog gue :). Slamat datang di weblog paling bermanfaat sedunia.
Dan gue doaian semoga orang-orang yang ngunjungin weblog gue pada masuk surga semua, trs selama hidupnya selalu di beri kemudahan, trs all the best deh buat kalian :D
Udah kaya ulang tahun aja ya ???.... Sorry ya klo penulis suka bercanda :)
Kembali lagi bersama gue muhamad pajar sidik, gue adalah seorang penulis blogger yang ganteng dan baik hati :D cieeee.....
Di hari yang indah ini alhamdulillah gue bisa nulis artikel kembali, yang mudah-mudahan artikel ini bisa bermanfaat buat kalian semua.
Kali ini gue bakalan nulis artikel tentang Rumus Permutasi Peluang , Tanpa panjang lebar lagi yo depository fiscal establishment jibe it out !

Matematika adalah ilmu yang paling banyak dipakai dalam kehidupan. Bahkan dalam kita bermain pun kita bisa menggunakan ilmu matematika. Contohnya dalam bermain kartu, untuk bermain kartu memang kita hanya bermain tanpa teknik pun bisa ikut main, namun pastinya kita akan slalu kalah dalam permainan tersebut. Nah biasanya orang - orang yang pandai dalam bermain kartu mereka menggunakan teknik-teknik tertentu, sehingga meraka akan slalu menjadi pemenang dalam permainan tersebut. Ilmu matematika peluang adalah ilmu yang sering sekali digunakan dalam permainan kartu dan permainan permainan lainnya. Nah kali ini saya akan berbagi rumus yang dasar dari materi peluang yaitu rumus "Permutasi".

Pengertian Permutasi 

Permutasi adalah "penyusunan kembali suatu objek dalam urutan yang berbeda dari urutan yang semula". Jadi intinya permutasi itu menyusun objek objek dengan uratan yang berbeda. 

Contoh :

Ada three objek :

1. A
2. B
3. C

Nah apabila disusun dalam urutan yang berbeda menjadi :

ABC, ACB, BCA, BAC, CBA, dan CAB

Nah maka ada iv urutan susunan yang berbeda. Jadi untuk menentukan permutasi itu yang perlu kita fokus adalah ke urutannya.

1. Rumus Permutasi Biasa

Keterangan :

P = Permutasi

n = banyaknya objek

k = printah banyaknya penyusunan objek

! = tanda bilangan victorial

Contoh :

Berapa bayak susunan yang terdiri atas iv huruf diambil dari huru-huruf T,O,S,E,R,B, dan H5N1 ?

Jawab :

n = {T,O,S,E,R,B, A} = 7

k = 4

maka :

2. Rumus Permutasi yang memuat unsur yang sama 

Keterangan :

P = Permutasi

n = banyaknya objek

a dan b dan seterusnya = objek-objek yang sama 

Contoh :

Cari lah objek permutasi dari 10 objek memuat ii objek yang sama, iv objek lainya yang sama dan three objek lainya sama !

Jawab :

n = 10 

a = 2

b = 4

c = 3

maka :

Kesimpulan

Jadi rumus permutasi itu ada dua, yang pertama permutasi biasa dan permutasi yang memuat unsur yang sama. Dan dalam mengoperasikan rumus permutasi kita harus tau dulu apa itu bilangan viktorial. Ya udah sebagai penjelas saya kasih tau deh jadi bilangan viktorial itu bilangan yang di tunjukan dengan simbol tada seru "!" dan bilangan viktorial itu adalah "bilangan utama dikali bilangan utama dikurang satu dikali bilangan utama dikurangi dua dan seterusnya sampai bilangan utama tersebut jika dikurangi bilangan seterusnya hasilnya satu". Contoh :

5! = v x (5-1) x (5-2) x (5-3) x( 5-4)

5! = v x iv x three x ii x 1 

5! = 120

Jadi 5! = 120

Nah segini dulu ya artikel kali ini. Baca juga artikel tentang :

• Rumus Kombinasi Peluang
• Rumus Frekuensi Harapan
• Rumus Peluang Suatu kejadian
• Rumus Komplemen Peluang 
• Rumus Peluang Kejadian Majemuk
• Rumus Peluang kejadian Bersyarat 

Mohon maaf apabila ada salah-salah kata

Akhir kata wassalamualaikum wr. wb.

Rumus Permutasi Peluang

Hallo temen-temen???
Pertama-tama gue ucapin trimakasih buat para pengunjung weblog gue :). Slamat datang di weblog paling bermanfaat sedunia.
Dan gue doaian semoga orang-orang yang ngunjungin weblog gue pada masuk surga semua, trs selama hidupnya selalu di beri kemudahan, trs all the best deh buat kalian :D
Udah kaya ulang tahun aja ya ???.... Sorry ya klo penulis suka bercanda :)
Kembali lagi bersama gue muhamad pajar sidik, gue adalah seorang penulis blogger yang ganteng dan baik hati :D cieeee.....
Di hari yang indah ini alhamdulillah gue bisa nulis artikel kembali, yang mudah-mudahan artikel ini bisa bermanfaat buat kalian semua.
Kali ini gue bakalan nulis artikel tentang Rumus Permutasi Peluang , Tanpa panjang lebar lagi yo depository fiscal establishment jibe it out !

Matematika adalah ilmu yang paling banyak dipakai dalam kehidupan. Bahkan dalam kita bermain pun kita bisa menggunakan ilmu matematika. Contohnya dalam bermain kartu, untuk bermain kartu memang kita hanya bermain tanpa teknik pun bisa ikut main, namun pastinya kita akan slalu kalah dalam permainan tersebut. Nah biasanya orang - orang yang pandai dalam bermain kartu mereka menggunakan teknik-teknik tertentu, sehingga meraka akan slalu menjadi pemenang dalam permainan tersebut. Ilmu matematika peluang adalah ilmu yang sering sekali digunakan dalam permainan kartu dan permainan permainan lainnya. Nah kali ini saya akan berbagi rumus yang dasar dari materi peluang yaitu rumus "Permutasi".

Pengertian Permutasi 

Permutasi adalah "penyusunan kembali suatu objek dalam urutan yang berbeda dari urutan yang semula". Jadi intinya permutasi itu menyusun objek objek dengan uratan yang berbeda. 

Contoh :

Ada three objek :

1. A
2. B
3. C

Nah apabila disusun dalam urutan yang berbeda menjadi :

ABC, ACB, BCA, BAC, CBA, dan CAB

Nah maka ada iv urutan susunan yang berbeda. Jadi untuk menentukan permutasi itu yang perlu kita fokus adalah ke urutannya.

1. Rumus Permutasi Biasa

Keterangan :

P = Permutasi

n = banyaknya objek

k = printah banyaknya penyusunan objek

! = tanda bilangan victorial

Contoh :

Berapa bayak susunan yang terdiri atas iv huruf diambil dari huru-huruf T,O,S,E,R,B, dan H5N1 ?

Jawab :

n = {T,O,S,E,R,B, A} = 7

k = 4

maka :

2. Rumus Permutasi yang memuat unsur yang sama 

Keterangan :

P = Permutasi

n = banyaknya objek

a dan b dan seterusnya = objek-objek yang sama 

Contoh :

Cari lah objek permutasi dari 10 objek memuat ii objek yang sama, iv objek lainya yang sama dan three objek lainya sama !

Jawab :

n = 10 

a = 2

b = 4

c = 3

maka :

Kesimpulan

Jadi rumus permutasi itu ada dua, yang pertama permutasi biasa dan permutasi yang memuat unsur yang sama. Dan dalam mengoperasikan rumus permutasi kita harus tau dulu apa itu bilangan viktorial. Ya udah sebagai penjelas saya kasih tau deh jadi bilangan viktorial itu bilangan yang di tunjukan dengan simbol tada seru "!" dan bilangan viktorial itu adalah "bilangan utama dikali bilangan utama dikurang satu dikali bilangan utama dikurangi dua dan seterusnya sampai bilangan utama tersebut jika dikurangi bilangan seterusnya hasilnya satu". Contoh :

5! = v x (5-1) x (5-2) x (5-3) x( 5-4)

5! = v x iv x three x ii x 1 

5! = 120

Jadi 5! = 120

Nah segini dulu ya artikel kali ini. Baca juga artikel tentang :

• Rumus Kombinasi Peluang
• Rumus Frekuensi Harapan
• Rumus Peluang Suatu kejadian
• Rumus Komplemen Peluang 
• Rumus Peluang Kejadian Majemuk
• Rumus Peluang kejadian Bersyarat 

Mohon maaf apabila ada salah-salah kata

Akhir kata wassalamualaikum wr. wb.

Rumus Permutasi Peluang

Hallo temen-temen???
Pertama-tama gue ucapin trimakasih buat para pengunjung weblog gue :). Slamat datang di weblog paling bermanfaat sedunia.
Dan gue doaian semoga orang-orang yang ngunjungin weblog gue pada masuk surga semua, trs selama hidupnya selalu di beri kemudahan, trs all the best deh buat kalian :D
Udah kaya ulang tahun aja ya ???.... Sorry ya klo penulis suka bercanda :)
Kembali lagi bersama gue muhamad pajar sidik, gue adalah seorang penulis blogger yang ganteng dan baik hati :D cieeee.....
Di hari yang indah ini alhamdulillah gue bisa nulis artikel kembali, yang mudah-mudahan artikel ini bisa bermanfaat buat kalian semua.
Kali ini gue bakalan nulis artikel tentang Rumus Permutasi Peluang , Tanpa panjang lebar lagi yo depository fiscal establishment jibe it out !

Matematika adalah ilmu yang paling banyak dipakai dalam kehidupan. Bahkan dalam kita bermain pun kita bisa menggunakan ilmu matematika. Contohnya dalam bermain kartu, untuk bermain kartu memang kita hanya bermain tanpa teknik pun bisa ikut main, namun pastinya kita akan slalu kalah dalam permainan tersebut. Nah biasanya orang - orang yang pandai dalam bermain kartu mereka menggunakan teknik-teknik tertentu, sehingga meraka akan slalu menjadi pemenang dalam permainan tersebut. Ilmu matematika peluang adalah ilmu yang sering sekali digunakan dalam permainan kartu dan permainan permainan lainnya. Nah kali ini saya akan berbagi rumus yang dasar dari materi peluang yaitu rumus "Permutasi".

Pengertian Permutasi 

Permutasi adalah "penyusunan kembali suatu objek dalam urutan yang berbeda dari urutan yang semula". Jadi intinya permutasi itu menyusun objek objek dengan uratan yang berbeda. 

Contoh :

Ada three objek :

1. A
2. B
3. C

Nah apabila disusun dalam urutan yang berbeda menjadi :

ABC, ACB, BCA, BAC, CBA, dan CAB

Nah maka ada iv urutan susunan yang berbeda. Jadi untuk menentukan permutasi itu yang perlu kita fokus adalah ke urutannya.

1. Rumus Permutasi Biasa

Keterangan :

P = Permutasi

n = banyaknya objek

k = printah banyaknya penyusunan objek

! = tanda bilangan victorial

Contoh :

Berapa bayak susunan yang terdiri atas iv huruf diambil dari huru-huruf T,O,S,E,R,B, dan H5N1 ?

Jawab :

n = {T,O,S,E,R,B, A} = 7

k = 4

maka :

2. Rumus Permutasi yang memuat unsur yang sama 

Keterangan :

P = Permutasi

n = banyaknya objek

a dan b dan seterusnya = objek-objek yang sama 

Contoh :

Cari lah objek permutasi dari 10 objek memuat ii objek yang sama, iv objek lainya yang sama dan three objek lainya sama !

Jawab :

n = 10 

a = 2

b = 4

c = 3

maka :

Kesimpulan

Jadi rumus permutasi itu ada dua, yang pertama permutasi biasa dan permutasi yang memuat unsur yang sama. Dan dalam mengoperasikan rumus permutasi kita harus tau dulu apa itu bilangan viktorial. Ya udah sebagai penjelas saya kasih tau deh jadi bilangan viktorial itu bilangan yang di tunjukan dengan simbol tada seru "!" dan bilangan viktorial itu adalah "bilangan utama dikali bilangan utama dikurang satu dikali bilangan utama dikurangi dua dan seterusnya sampai bilangan utama tersebut jika dikurangi bilangan seterusnya hasilnya satu". Contoh :

5! = v x (5-1) x (5-2) x (5-3) x( 5-4)

5! = v x iv x three x ii x 1 

5! = 120

Jadi 5! = 120

Nah segini dulu ya artikel kali ini. Baca juga artikel tentang :

• Rumus Kombinasi Peluang
• Rumus Frekuensi Harapan
• Rumus Peluang Suatu kejadian
• Rumus Komplemen Peluang 
• Rumus Peluang Kejadian Majemuk
• Rumus Peluang kejadian Bersyarat 

Mohon maaf apabila ada salah-salah kata

Akhir kata wassalamualaikum wr. wb.

Rumus Permutasi Peluang

Hallo temen-temen???
Pertama-tama gue ucapin trimakasih buat para pengunjung weblog gue :). Slamat datang di weblog paling bermanfaat sedunia.
Dan gue doaian semoga orang-orang yang ngunjungin weblog gue pada masuk surga semua, trs selama hidupnya selalu di beri kemudahan, trs all the best deh buat kalian :D
Udah kaya ulang tahun aja ya ???.... Sorry ya klo penulis suka bercanda :)
Kembali lagi bersama gue muhamad pajar sidik, gue adalah seorang penulis blogger yang ganteng dan baik hati :D cieeee.....
Di hari yang indah ini alhamdulillah gue bisa nulis artikel kembali, yang mudah-mudahan artikel ini bisa bermanfaat buat kalian semua.
Kali ini gue bakalan nulis artikel tentang Rumus Permutasi Peluang , Tanpa panjang lebar lagi yo depository fiscal establishment jibe it out !

Matematika adalah ilmu yang paling banyak dipakai dalam kehidupan. Bahkan dalam kita bermain pun kita bisa menggunakan ilmu matematika. Contohnya dalam bermain kartu, untuk bermain kartu memang kita hanya bermain tanpa teknik pun bisa ikut main, namun pastinya kita akan slalu kalah dalam permainan tersebut. Nah biasanya orang - orang yang pandai dalam bermain kartu mereka menggunakan teknik-teknik tertentu, sehingga meraka akan slalu menjadi pemenang dalam permainan tersebut. Ilmu matematika peluang adalah ilmu yang sering sekali digunakan dalam permainan kartu dan permainan permainan lainnya. Nah kali ini saya akan berbagi rumus yang dasar dari materi peluang yaitu rumus "Permutasi".

Pengertian Permutasi 

Permutasi adalah "penyusunan kembali suatu objek dalam urutan yang berbeda dari urutan yang semula". Jadi intinya permutasi itu menyusun objek objek dengan uratan yang berbeda. 

Contoh :

Ada three objek :

1. A
2. B
3. C

Nah apabila disusun dalam urutan yang berbeda menjadi :

ABC, ACB, BCA, BAC, CBA, dan CAB

Nah maka ada iv urutan susunan yang berbeda. Jadi untuk menentukan permutasi itu yang perlu kita fokus adalah ke urutannya.

1. Rumus Permutasi Biasa

Keterangan :

P = Permutasi

n = banyaknya objek

k = printah banyaknya penyusunan objek

! = tanda bilangan victorial

Contoh :

Berapa bayak susunan yang terdiri atas iv huruf diambil dari huru-huruf T,O,S,E,R,B, dan H5N1 ?

Jawab :

n = {T,O,S,E,R,B, A} = 7

k = 4

maka :

2. Rumus Permutasi yang memuat unsur yang sama 

Keterangan :

P = Permutasi

n = banyaknya objek

a dan b dan seterusnya = objek-objek yang sama 

Contoh :

Cari lah objek permutasi dari 10 objek memuat ii objek yang sama, iv objek lainya yang sama dan three objek lainya sama !

Jawab :

n = 10 

a = 2

b = 4

c = 3

maka :

Kesimpulan

Jadi rumus permutasi itu ada dua, yang pertama permutasi biasa dan permutasi yang memuat unsur yang sama. Dan dalam mengoperasikan rumus permutasi kita harus tau dulu apa itu bilangan viktorial. Ya udah sebagai penjelas saya kasih tau deh jadi bilangan viktorial itu bilangan yang di tunjukan dengan simbol tada seru "!" dan bilangan viktorial itu adalah "bilangan utama dikali bilangan utama dikurang satu dikali bilangan utama dikurangi dua dan seterusnya sampai bilangan utama tersebut jika dikurangi bilangan seterusnya hasilnya satu". Contoh :

5! = v x (5-1) x (5-2) x (5-3) x( 5-4)

5! = v x iv x three x ii x 1 

5! = 120

Jadi 5! = 120

Nah segini dulu ya artikel kali ini. Baca juga artikel tentang :

• Rumus Kombinasi Peluang
• Rumus Frekuensi Harapan
• Rumus Peluang Suatu kejadian
• Rumus Komplemen Peluang 
• Rumus Peluang Kejadian Majemuk
• Rumus Peluang kejadian Bersyarat 

Mohon maaf apabila ada salah-salah kata

Akhir kata wassalamualaikum wr. wb.

Rumus Peluang

Sebelumnya kita pasti bertanya-tanya dulu, apa sih peluang itu??
apa sih kegunaannya??

Nah prihal hal di atas peluang itu adalah suatu perikaraan atau pun prediksi mengenai suatu kejadia yang akan terjadi atau pun belum terjadi. Kegunaanya yaitu sebenarnya banyak manusia yang memanfaatkakn ilmu peluang ini dengan perbuatan yang tedak baik contohnya seperi berjudi. Akan tetapi ilmu peluang ini sangat penting bagi dunia ini seperti BMKG(badan matereologi klimatologi dan geofisika) untuk memprediksikan apakah cuaca pada hari esok atau beberapa detik yang akan datang akan terjadi hujan atau kah tidak. Nah namun dalam ilmu ekonomi peluang juga dapat menetukan apakah seorang enterprener harus mengambil usaha tersebut atau kah tidak. Mungkin hanya segitu saja yh sekilah penerangan mengenai apakah itu peluang dan apa keguanaanya.

            Sebelum kita masuk lebih jauh terhadap materi peluang, kita harus terlebih dahulu mengetahui apakah itu sampel dan ruang sampel. Sampel adalah bagian dari ruang sampel dan ruang sampel adalah jumlah keseluruhan dari information tersebut..

Kaidah pencacahan ( Caunting Slots)

            Kaidah pecacahan adalah suatu kadiah yang digunakan untuk menentukan atau menghitung berapa bayak cara yang terjadi dalam suatu peristiwa.
Kaidah Pencacahan terdiri atas :

A.      Pengisian tempat yang tersedia (Filling SlotS)

B.      Permutasi dan,

C.      Combinasi

Untuk yang pertama pengisian tempat kita tidak perlu mengetahui rumus namun kita lansung ke contoh saja yah :

Misalkan kita mempunya tiga angka 1,2,3 dan kita akan membuat dua bilangan dari angka tersebut maka banyak bilangan yang kita buat  ada….

Jawaban:
ada dua digit angka angka yang kita harus buat (_ _) untuk digit pertama kita dapat isikan oleh ketiga angka tersebut namun untuk digit kedua hanya bisa diisi oleh two digit angka saja karena angka sudah terpakai i digit untuk digit yang pertama maka :

3 2, maka iii x two = vi jadi ada enam angka yang dapa kita buat dari angka angka tersebut. {12,13,21,23,31,32}

§      PERMUTASI

Namun sebelum kita belajar permutasi kita harus faham dulu mengenai notasi factorial. Notasi factorial adalah hasil kali dari bilangan bulat positif dari i sampai ke n. notasi factorial dilambangkan dengan n! ( dibaca “ n factorial “)

Rumus :

Contoh :

Nah sekarang kita belajar permutasi  namanya juga permutasi jadi untuk setiap mutasi atau perpindahan objek dari suatu datat di hitung. Contohnya AB dan BA dianggap berbeda.

Rumus :

Contoh :

Berapa bayak susunan yang terdiri atas four huruf diambil dari huru-huruf T,O,S,E,R,B, dan Influenza A virus subtype H5N1 ?

Jawaban :

Maka ada 840 susunan angka yang dapat di bentuk .

           

Namun ada pun permutasi yang memuat unsure yang sama seperti M,T,M di situ ada dua huruf yang sama yaitu M.  adapun rumus permutasi dengan unsur yang berbeda :

Contoh :

Cari lah objek permutasi dari 10 objek memuat two objek yang sama, four objek lainya yang sama dan iii objek lainya sama !

Jawab :

§      COMBINASI

Untuk kombinasi berkebalikan dengan permutasi jika AB, BA dalam permutasi dihitung berbeda maka dalam combinasi dihitung sama saja. Rumus :

Contoh :

Dari suatu kotak terdapat xx bola dimana 8 warnanya merah, vii warnanya putih, dan sisanya berwarna hitam. Jika diambil four bola dari kotak tersebut, berapakah banyak cara untuk medapatkan warna dua merah dan dua putih?

Jawab:

§      PELUANG KEJADIAN

Nah untuk mempelajari peluang sebaiknya ingat-ingat lagi yah apa itu pengertia sampel, ruang sampel, dan sebagainya.

Sebelum mengetahui pengertian peluang kita harus tau apakah itu frekuensi relative. Frekuensi relative adalah perbandaingan antara banyaknya hasil yang muncul dengan banyaknya percobaan yang dilakukan.

Namun peluang adalah nilai munculnya anggot suatu kejadian dibandingkan dengan banyaknya anggota seluruh kejadian. Rumus :

P(A) : Peluang munculnya suatu kejadian A
n(A) : Banyaknya anggota dalam kejadian A
n(S) : Banyaknya anggota dalam himpunan ruang sampel.

Contoh :

Pada pelemparan sebuah dadu, tentukanlah peluang kejadian munculnya bilangan two ?

Jawab :

S= {1,2,3,4,5,6} maka n(S) = 6
dan mata dadu two hanya da 1, n (A) = i maka ;

§      FREKUESI HARAPAN

Frekuensi harapan adalah hasil kali peluang P(A) dengan banyaknya percobaan :

Contoh :

Tiga buah uang logam yang berisi gambar (G) dan angka (A) di lempar bersama-sama sebanyak lxxx kali, tentukan harapan  munculnya tiga-tiganya angka ?

Jawab :

S={GGG,GGA,GAG,AGG,AAG,AGA,GAA,AAA} n(S)=8
untuk tiga-tiganya angka A={AAA), n(A)=1 sehingga :

§      PELUANG KOMPLEMEN SUATU KEJADIAN

Banyaknya kejadian komplemen atau kejadian bukan Influenza A virus subtype H5N1 dilambangkan atau di rumuskan dengan:

Contoh :

Peluang bahwa hari esok hujan adalah 0,26. Tentukan peluang bahwa hari esok hari tidak hujan!

Jawab :

§      PELUANG KEJADIAN MAJEMUK

Aturan penjumlahan dalam kejadian majemuk

            Misakan pada percobaan melempar dadu berisi enam sebanyak satu kali. Muncul bilangan prima, yaitu Influenza A virus subtype H5N1 = { 2,3,5} dan kejadian B muncul bilangan genap, yaitu B {2,4,6,). Dalam diagram Venn dua kejadian diatas dapat dilukiskan sebagai berikut :

Maka di gunakan rumus :

Maka ini di sebut dengan kejadian tidak saling lepas atau saling asing

Untuk kejadian yang saling lepas atau saling asing di gunakan rumus :

dikarenakan P(AnB) = 0

Contoh dari aturan penjumlahan :

Sebuah dadu dilempar sekali, berapa munculnya bilangan <=2 atau >=5 ?

Jawab :

§      ATURAN PERKALIAN DALAM PELUANG KEJADIAN MAJEMUK     

Kejadian Influenza A virus subtype H5N1 dan B saling bebas jika dan hanya jika :

Dan kejadian tidak saling bebas :

Saya rasa mengenai hal di atas tidak perlu saya beri contoh

§      KEJADIAN BERSYARAT

Kejadian bersyarat atau kejadian tidak saling bebas dirumuskan dengan :

Contoh :

Dari seperangkat kartu bridge, diambil satu per satu dua kali tanpa pengembalian, tentukan peluang munculnya dua duanya kartu merah !

Jawab :

Sekian saja yh materi dari matematika akuntansi.

Mohon maaf apabila ada kesalahan dan silahkan komentari jika ada yang salah pada spider web log ini

oh iyh dan terakhir guys buat latihan soalnya nih ngerjain di link ini :
https://ginabortolussiblog.blogspot.com//search?q=latihan-materi-peluang

Akhir kata saya fajar sidik wasalamualaikum Wr. Wb.