Hallo guys ??
Kali ini gw bakalan posting materi tentang Pencerminan Transformasi Bangun Datar atau Refleksi
Simak baik-baik yah guys !
Pengertian
Pencerminan (Refleksi) adalah suatu transformasi yang memindahkan setiap titik pada bidang dengan dengan menggunakan sifat bayangan cermim.
Macam - Macam Pencerminan
Ada beberapa macam pencerminan dalam ilmu transformasi bangun datar, yaitu :
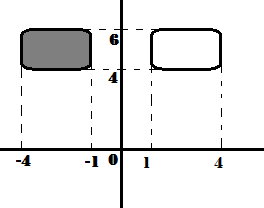
a. Pencerminan terhadap sumbu x
Dari gambar diatas, persegi panjang warna abu" merupakan bayangan dari persegi putih terhadap sumbu x.
Rumus pencerminan terhadap sumbu x adalah :
A(x,y) → x = A' (x, -y) Keterangan :
A : titik A
A' : titik H5N1 setelah pencerminan
x : titik pada sumbu x
y : titik pada sumbu y
→ x: pencerminan terhadap sumbu x
Contoh :
titik dari titik (1,4) yang dicerminkan terhadap sumbu x adalah ?
Jawab :
x = 1
y = 4
A(x,y) → x = A' (x,-y)
A(1,4) → x = A' (1,-4)
Maka hasil pencerminan dari titik (1,4) terhadap sumbu x adalah (1,-4) dan untuk membuktikannya lihat saja pada gambar di atas.
b. Pencerminan terhadap sumbu y
Dari gambar sebelah kiri, persegi panjang warna abu-abu adalah hasil dari pencerminan persegi panjang warna putih terhadap sumbu y.
Rumus pencerminan terhadap sumbu y adalah :
A(x,y) → y = A' (-x, y) Keterangan :
A : titik A
A' : titik H5N1 setelah pencerminan
x : titik pada sumbu x
y : titik pada sumbu y
→ y: pencerminan terhadap sumbu y
Contoh :
titik dari titik (1,4) yang dicerminkan terhadap sumbu y adalah ?
Jawab :
x = 1
y = 4
A(x,y) → y = A' (-x,y)
A(1,4) → y = A' (-1,4)
Maka hasil pencerminan dari titik (1,4) terhadap sumbu y adalah (-1,4) dan untuk membuktikannya lihat saja pada gambar di atas.
c. Pencerminan terhadap sumbu y = k
Dari gambar di samping, persegi panjang warna abu-abu adalah bayangan dari persegi panjang warana putih terhardap garis sumbu y = 1.
Rumus pencerminan terhadap sumbu y = k adalah :
A(x,y) → y : k = A' (x, 2h - y) Keterangan :
A : titik A
A' : titik H5N1 setelah pencerminan
x : titik pada sumbu x
y : titik pada sumbu y
k : bilangan dari sumbu y
→ x : h : pencerminan terhadap sumbu y = k
Contoh :
titik dari titik (1,4) yang dicerminkan terhadap sumbu y = one adalah ?
Jawab :
x = 1
y = 4
A(x,y) → y:k = A' (x , 2h - y)
A(1,4) → y:1 = A' (1,2(1)-4)
= A' (1, 2-4 )
= A' (1, -2 )
Maka hasil pencerminan dari titik (1,4) terhadap sumbu y = one adalah (1,-2) dan untuk membuktikannya lihat saja pada gambar di atas.
d. Pencerminan terhadap sumbu x = h
Dari gambar di samping, persegi warna abu-abu adalah bayang dari pencerminan persegi warna putih terhadap gari x = -1.
Rumus pencerminan terhadap sumbu x = h adalah :
A(x,y) → x : h = A' (2k - x, y) Keterangan :
A : titik A
A' : titik H5N1 setelah pencerminan
x : titik pada sumbu x
y : titik pada sumbu y
h : bilangan dari sumbu x
→ x : h : pencerminan terhadap sumbu x = h
Contoh :
titik dari titik (1,4) yang dicerminkan terhadap sumbu x = -1 adalah ?
Jawab :
x = 1
y = 4
A(x,y) → x:h = A' ( 2k - x , y)
A(1,4) → x:-1 = A'( 2(-1) - one , 4)
= A' (-2 - 1, four )
= A' (-3, four )
Maka hasil pencerminan dari titik (1,4) terhadap sumbu y = -1 adalah (-3,4) dan untuk membuktikannya lihat saja pada gambar di atas.
e. Pencerminan terhadap titik pangkal
Dari gambar di samping, persegi panjang warna abu-abu adalah bayangan dari persegi panjang warana putih terhardap titik pangkal (0,0)
Rumus pencerminan terhadap titik pangkal adalah :
A(x,y) → (0,0) = A' (-x, - y) Keterangan :
A : titik A
A' : titik H5N1 setelah pencerminan
x : titik pada sumbu x
y : titik pada sumbu y
→ (0,0) : pencerminan terhadap titik pangkal
Contoh :
titik dari titik (1,4) yang dicerminkan terhadap titik pangkal adalah ?
Jawab :
x = 1
y = 4
A(x,y) → (0,0) = A' (-x, - y)
A(1,4) → (0,0) = A' (-1, - 4)
= A' (-1 , -4 )
= A' (-1 , -4 )
Maka hasil pencerminan dari titik (1,4) terhadap titik pangkal adalah (-1,-4) dan untuk membuktikannya lihat saja pada gambar di atas.
f. Pencerminan terhadap garis x = y
Dari gambar di samping, persegi panjang warna abu-abu adalah bayangan dari persegi panjang warana putih terhardap garis y = x
Rumus pencerminan terhadap sumbu y = x adalah :
A(x,y) → y=x = A' (y,x) Keterangan :
A : titik A
A' : titik H5N1 setelah pencerminan
x : titik pada sumbu x
y : titik pada sumbu y
→y=x: pencerminan terahadap garis y = x
Contoh :
titik dari titik (3,8) yang dicerminkan terhadap garis y = x adalah ?
Jawab :
x = 3
y = 8
A(x,y) → y=x = A' (y,x)
A(3,8) → y=x = A' (8, 3)
Maka hasil pencerminan dari titik (3,8) terhadap garis y = x adalah (8,3) dan untuk membuktikannya lihat saja pada gambar di atas.
g. Pencerminan terhadap garis y = -x
Dari gambar di samping, persegi panjang warna abu-abu adalah bayangan dari persegi panjang warana putih terhardap garis y = -x
Rumus pencerminan terhadap sumbu y = x adalah :
A(x,y) → y=-x = A' (-y,-x) Keterangan :
A : titik A
A' : titik H5N1 setelah pencerminan
x : titik pada sumbu x
y : titik pada sumbu y
→y= - x: pencerminan terahadap garis y = -x
Contoh :
titik dari titik (3,8) yang dicerminkan terhadap garis y = -x adalah ?
Jawab :
x = 3
y = 8
A(x,y) → y= -x = A' (-y, -x)
A(3,8) → y= -x = A' (-8, -3)
Maka hasil pencerminan dari titik (3,8) terhadap garis y = x adalah (-8,-3) dan untuk membuktikannya lihat saja pada gambar di atas.
h. Pencerminan terhadap titik P(a,b)
Dari gambar di samping, persegi panjang warna abu-abu adalah bayangan dari persegi panjang warana putih terhardap titik P(a,b)
Rumus pencerminan terhadap sumbu y = x adalah :
A(x,y) → P(a,b) = A' (2a-x , 2b-y) Keterangan :
A : titik A
A' : titik H5N1 setelah pencerminan
x : titik pada sumbu x
y : titik pada sumbu y
→P(a,b): pencerminan terahadap titik P(a,b)
Contoh :
titik dari titik (3,8) yang dicerminkan terhadap titik P(11,8) adalah ?
Jawab :
x = 3
y = 8
a = 11
b = 8
A(,y) → P(a,b) = A' (2a-x , 2b-y)
A(x,y) → P(11,9) = A' (2(11)-3 , 2(8)-8)
= A' (22-3 , 16-8)
= A' (19 , 8)
Maka hasil pencerminan dari titik (3,8) terhadap garis y = x adalah (19,8) dan untuk membuktikannya lihat saja pada gambar di atas.
Nah segini dulu yah materi dari saya
Untuk menambah pemahamam baca juga artikel tentang :
mohon maaf jika ada kesalahan
assalamualaikum good daytime bye........