Rumus Integral Tertentu Dan Contohnya

Assalamualiakum everyone ???

Dalam matematika itu dua integral, diantaranya adalah integral tertentu dan integal tak tentu. Integral tertentu adalah integral yang sudah ditentukan nilai x nya sedangkan integral tak tentu sebaliknya.

Kali ini saya akan berbagi artikel tentang integral tertentu berikut contohnya.

Mengapa harus belajar integral tak tentu ???

Manfaat Integral Tertentu

Integral tertentu digunakan untuk menghitung luas dari suatu kurva. Jadi dengan rumus integral tertentu kita dapat menghitung luas dari sebuah kurva.

Rumus Integral Tertentu

Rumus :

_a∫^b f'(x) dx = [F(x)]^b_a = f(b) - f(a)

Keterangan  :

a dan b = nilai x yang telah ditentukan
∫ = integral
x = variabel
f'(x) = turunan dari x
dx = dibaca turunan x

Contoh Soal Integral Tertentu

Berapakah hasil dari ₁∫³ 3x² dx = ... ?

Jawaban :

₁∫³ 3x² dx = [3/3(x³)]³_1
1∫³ 3x² dx = [x³]³_1
1∫³ 3x² dx = (3³) - (1³)
₁∫³ 3x² dx = 27 - 1
₁∫³ 3x² dx = 26

Sekian artikel kali ini. Mohon maaf apabila ada salah-salah kata.

Akhir kata wassalamualaikum wr. wb.

Referensi :

• Chanel youtube sibejoo jadda

Belajar Kalkulus Dasar

What is Kalkulus .... ??

Hallo teman-teman berjumpa lagi dengan saya si blogger ganteng :)

Kali ini saya bakalan berbagi sedikit ilmu tentang kalkulus.

Apa itu kalkulus ... ???

Kalkulus dalam bahasa latin adalah calculus yang artinya "batu kecil", untuk menghitung. Kalkulus adalah cabang ilmu matematika yang mencakup limit, turunan, integral, dan deret takterhingga. (https://id.wikipedia.org/wiki/Kalkulus)

Jadi ketika kita belajar deret tak hingga di SMP dan belajar limit, turunan, dan integral di SMA/SMK maka artinya kita sedang mempelajari materi Kalkulus.

Kalkulus adalah ilmu yang mempelajari perubahan, seperti halnya geometri yang mempelajari bentuk dan aljabar yang mempelajari operasi dan penerapannya untuk memecahkan persamaan. Sir Isaac Newton adalah salah seorang penemu dan kontributor kalkulus yang terkenal dan Gottfried Wilhelm Leibniz pada awalnya dituduh menjiplak dari hasil kerja Sir Isaac Newton yang tidak dipublikasikan, namun sekarang dianggap sebagai kontributor kalkulus yang hasil kerjanya dilakukan secara terpisah.

Kalkulus memiliki dua cabang utama, kalkulus diferensial dan kalkulus integral yang saling berhubungan melalui teorema dasar kalkulus. Maka dari itu untuk bisa faham dasar kalkulus kita harus mempelajari diferensial dan integral.

DIFERENSIAL

Apa itu diferensial ..???

Kalkulus diferensial adalah salah satu cabang ilmu kalkulus yang mempelajari bagaimana nilai suatu fungsi berubah menurut perubahan input nilainya. Topik utama dalam pembelajaran kalkulus diferensial adalah turunan. (https://id.wikipedia.org/wiki/Kalkulus)

Turunan dari suatu fungsi pada titik tertentu menjelaskan sifat-sifat fungsi yang mendekati nilai input. Untuk fungsi yang bernilai existent dengan variabel existent tunggal, turunan pada sebuah titik sama dengan kemiringan dari garis singgung grafik fungsi pada titik tersebut. Secara umum, turunan suatu fungsi pada sebuah titik menentukan pendekatan linear terbaik fungsi pada titik tersebut.

RUMUS TURUNAN PERTAMA

Misalnya  y merupakan fungsi dari x atau dapat ditulis juga y = f(x). Turunan dari y terhadap x dinotasikan sebagai berikut:

dy/dx = Cnx^n-1

Contoh soal :

y = 2x⁴

Jawaban :

dy/dx = two . 4x^4-1 

dy/dx = 8x³

Jadi turunan dari y = 2x⁴ adalah 8x³.

Untuk rumus turunan kedua atau seterusnya, mungkin nanti akan saya bahas di artikel berikutnya. Jika teman-teman ingin cepat cepat mempelajarinya bisa cari di sumber lain.

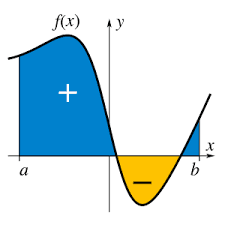
INTEGRAL

Apa itu integral.. ?

Integral adalah sebuah konsep penjumlahan secara berkesinambungan dalam matematika, dan bersama dengan inversnya, diferensiasi, adalah satu dari dua operasi utama dalam kalkulus. (https://id.wikipedia.org/wiki/Integral)

Integral dikembangkan menyusul dikembangkannya masalah dalam diferensiasi yang dimana matematikawan harus berpikir bagaimana menyelesaikan masalah yang berkebalikan dengan solusi diferensiasi.

Ada dua macam integral yaitu integral tak tentu, dan integral tentu. Integral tak tentu adalah integral yang belum ditentukan nilai variabelnya, sedangkan integral tentu adalah integral yang telah ditentukan variabelnya.

RUMUS INTEGRAL TAK TENTU

∫ ax² dx = (a/(n+1))xⁿ⁺¹ + C

Keterangan :

∫ : Integral 

a : koefisen x 

x : variabel a 

n : pangkat fungsi f(x) 

C : konstanta

Contoh :

Berapakah hasil dari ∫ x² dx = ... ?

Jawaban :

a = 1

n = 2

∫ ax² dx = (a/(n+1))xⁿ⁺¹ + C 

∫ x² dx = (1/(2+1))x²⁺¹ + C 

∫ x² dx = (1/3)x³ + C

Jadi hasil dari ∫ x² dx adalah (1/3)x³ + C.

Untuk Integral tantu bisa teman-teman lihat selangkapnya pada link di bawah ini :

https://ginabortolussiblog.blogspot.com//search?q=rumus-integral-tertentu-dan-contohnya

Sekian artikel kali ini. Mohon maaf apabila ada salah-salah kata.

Akhir kata wassalamualaikum wr. wb.

Referensi :

• https://id.wikipedia.org/wiki/Kalkulus
• https://id.wikipedia.org/wiki/Integral