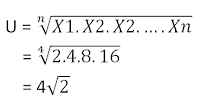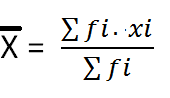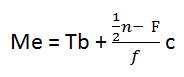Home Posts filed under Search results for rumus-rata-rata-mean-median-modus-data-kelompok
Showing posts sorted by relevance for query rumus-rata-rata-mean-median-modus-data-kelompok. Sort by date Show all posts
Showing posts sorted by relevance for query rumus-rata-rata-mean-median-modus-data-kelompok. Sort by date Show all posts

Rumus Rata-Rata (Mean), Median, Dan Modus Information Tunggal (Statistik)

Nih guys gw punya ilmu tentang bagaimana caranya menghitung Rata-Rata, Median, dan Modus information tunggal.
Simak yah guys !!!!!
1. Rumus Rata-Rata Data tunggal 
Dalam kehidupan sehari-hari, rata-rata lebih banyak dikenal, misalnya rata-rata gaji pegawai suatu perusahaan tiap bulan.
Nilai rata-rata yang akan dibahas dalam artikel ini meliputi rata-rata hitung, rata-rata ukur ( Rata-Rata Geometrik ), dan rata-rata harmonik.
a. Rumus Rata-Rata hitung information tunggal
Dari sekumpulan information X1,X2,X3,...,,Xn, maka rata-rata hitung dari information tersebut adalah :
       
keterangan : n = Banyak data
contoh :
tentukan nilai rata-rata hitung dari information 6,4,8,10,11,10,7

Jawab :
b. Rumus Rata-Rata Ukur ( Rata-Rata Geometrik)
Jika perbandingan tiap dua information berurutan tetap atau hampir tetap, rata-rata ukur lebih baik digunakan dari pada rata-rata hitung, apabila kehendaki rata-ratanya.
Rumus :

Contoh ; 
Hitunglah rata-rata ukur information berikut : 2,4,8,16!
Jawab :
 
c. Rata-Rata Harmonik
       Rumus :

Contoh :
Hitunglah rata-rata Harmonik dari information berikut : 3,5,6,6,7,10,12!
Jawab :



2. Rumus Modus Data Tunggal (Mo)
Modus dari suatu information adalah information yang sering muncul atau information yang mempunyai frekuensi tertinggi.
Contoh :
Tentukan Modus information berikut : 3,4,4,5,5,5,6,7
Jawab :
Modus information tersebut adalah 5

3. Rumus Median Data tunggal
Median (Me) adalah nilai pertengahan dari sekelompok information yang telah diurutkan menurut besarnya.
Rumus :
   a. Jika banyak information ganjil :
Contoh :
Tentukan median dari information :
3,7,6,4,5
Jawab :
maka kita urutkan terlebih dulu datanya menjadi 3,4,5,6,7
maka mediannya : information ke ; (n+1)/2 = (5+1)/2 = 3
Maka information ke-3 adalah 5

     b. Jika bayak datanya genap :


Contoh :
Tentukan median dari information ;
1,2,4,3
Jawab ;
Maka kita urutkan dahulu datnya :
Data ke-(n/2)+  data ke-((n/2)+1)/2 = information ke-(4/2)+data ke((4/2)+1/2
                                                         =(data ke-2 + Data ke-3)/2
                                                         =       (2 + 3)/2
                                                         = 2,5


Nah segini dulu yah materinya
Untuk menambah pemahaman baca juga artikel tentang :

Rumus Rata-Rata (Mean), Median, Dan Modus Information Kelompok (Statistik)

Hallo temen-temen??
Pertama-tama gue ucapin trimaskasih ama temen-temen yang udah ngunjungin weblog gue. Jujur gue seneng banget kalo ada orang yang berkunjung ke weblog gue.
Kembali lagi bersama gue pajar seorang penulis weblog ganteng :D.
kli ini gw bakalan nge shere materi tentang Rumus Rata-Rata (Mean), Median, dan Modus Data Kelompok (Statistik).
Dulu gue belajar materi ini di kelas 12 smk ya temen-temen, pelajaran ini cukup gampang ko.
y udah simak ya!!!!!!! 

1. Rumus Rata-Rata Hitung information kelompok (Mean) 
Rumus :

Keterangan :
fi = frekuensi
11 = nilai tengah
Nilai tengah adalah jumlah tepi bawah dan tepi atas di bagi 2
Contoh :
Perhatikan tabel berikut :
dari tabel berikut tentukan rata-rata hitungnya!
Jawab :
x̅ = (Σ fi . 11 )/Σ fi 
x̅ = 535/40
x̅ = 13,38

2. Rumus Modus Data Kelompok
Rumus :
Keterangan :
Tb = Tepi bawah kelas modus
d1 = Selisih antara frekuensi modus dengan frekuensi sebelumnya
d2 = selisih antara frekuensi modus dengan frekuensi sesudahnya
c = Panjang kelas

Contoh :
Perhatikan tabel berikut :
tentukan modus dari tabel diatas !
Jaawab :
Tb = 45 -0,5 = 44,5
d1 = 17 - xiii  = 4
d2 = 17 - xiv  = 3
c = 35 - xxx = 5

Mo = Tb + (d1/(d1 + d2))c
Mo = 44,5 + (4/(3 + 4))5
Mo = 44,5 + 20/7
Mo = 47,35

3. Rumus Median Data Kelompok
rumus :
Keterangan :
Tb = Tepi bawah kelas median
F = Jumlah frekuensi sebelum median
f  = Frekuensi
c = Panjang kelas
n = Jumlah frekuensi

Contoh :
perhatikan tabel di bawah

Tentukan median dari tabel di atas :
Jawab :
Tb = 45 - 0,5 = 44,5
n   = 80
F   = 8 + 10 + xiii = 31
c   = 5
f    = 17

Me = Tb + ( (1/2 n - F)/f )c
Me = Tb + ( (1/2 80 - 31)/17 )5
Me = Tb + ( 9/17 )5  
Me = 47,15
Nah segini dulu yah materi dari saya
asalamualaikum cheerio bye......

Cara Menyajikan Tabel Distribusi Frekuensi Information Kelompok

Hallo guys.......!!!
Kli ini gw punya artikel tentang gimana caranya nyajiin tabel distribusi frekuensi information kelompok.
Simak ya!!!!!

Data yang telah dikumpulkan, baik dari populasi maupun sampel untuk keperluan laporan dan atau analisis selanjutnya, perlu diatur, disusun, dan disajikan dalam bentuk yang jelas dan baik. Secara garis besar penyajian information dibagi menjadi dua cara yaitu dalam bentuk tabel dan grafik.

Dalam menyajikan tabel information klompok itu kadang beberapa bagian orang merasa kesulitan karena mereka berfikir untuk menyusun satu persatu dahulu dari banyak datang yang mereka dapatkan.
Padaha jika mereka tau ilmunya mereka tidak akan kebingungan seperti itu. Maka dari saya akan berbagi ilmunya.

Nah berikut cara meyajikan tabel distribusi frekuensi information kelompok :
1. Langkah yang pertama kita surfey nilai lxxx siswa :
    Data Untuk lxxx siswa :
    lxxx 80 lxx 68 xc 92 lxxx lxx 63 76
    49 84 71 72 35 93 91 74 lx 63
    48 xc 92 85 83 76 61 99 83 88
    74 lxx 38 51 73 71 72 95 82 70
    81 91 56 65 74 xc 97 lxxx lx 66
    98 93 81 93 43 72 91 59 67 88
    87 82 74 83 86 67 88 71 89 79
    82 78 73 86 68 75 81 77 63 75

2. Tentukan rentangan (R) !
     Rentangan (R) = Nilai terbesar - Nilai terkecil
                  R  = 99 - 35
                       = 64

3. Tentukan Banyaknya kelas untuk interval tabel!
Banyaknya Kelas (k) = 1 + 3,3 log n
                                    k  = 1 + 3,3 log 80
                                         = one  + (3,3) (1,9031)
                                         = 7,2802
ket : n = banyaknya data
Maka kita dapat membuat daftar dengan banyaknya kelas seven atau 8

4. Tentukan panjang kelas interval !
     P = R/k
        = 64/7
        = 9,14
Maka panjang kelas dapat kita ambil nine atau 10

5. Tentukan batas bawah kelas interval pertama !
Batas bawah interval kelas pertama dapat diambil dari information yang terkecil atau information yang lebih kecil dari information terkecil tetapi selisihnya kurang dari panjang kelas dan kelas pertama tidak boleh
mempunyai frekuensi sama dengan nol.
maka saya ambil saja batas bwah interval pertamanya adalah 31

6. Amati berapa banyak angka yang sama (turus) pada setiap kelas dan tulis pada kolom turus dengan tanda (I)

7. Isi jumlah frekuensi sesuai banyaknya turus.
Maka akan di peroleh tabel distribusi frekuensi sebagai berikut :

nah guys sambil coba yah bikin sendiri
Segini dulu yah materi dari saya ntar klo panjang-panjang malah bikin bingung lagi
Asslamualaikum farewell bye.....

Ukuran Penyebaran Information (Dispersi)

how r u guys?
Kali ini gw bakalan kasih kalian ilmu tentang penyebaran data.
Simak ya !

Ada beberapa ukuran penyebaran information (dispersi), antara lain

1. Jangkauan/Range (R)
     Ukuran penyebaran information yang paling mudah adalah range. Apabila sekumpulan information sudah tersusun dari yang terkecil hingga yang terbesar, maka make dari information adalah selisih information terbesar (X-max) dengan information terkecil (X-min)
Maka diperoleh rumus :
                                       R = (X-max - X-min)
Contoh :
Tentukan make dari information 20,30,35,40,50,56,60 !
Jawab :
X-max = 60
X-min = 20

R = (X-max - X-min)
    = lx - 20
    = 40

Maka rangenya adalah 40

2. Rata-Rata Simpangan (RS)














3. Simpangan Baku (Deviasi Standar)
Barangkali ukuran simpangan baku yang paling banyak digunakan adalah simpangan baku atau deviasi setandar, karena mempunyai sifat-sifat matematik (mathematical property) yang sangat penting dan berguna untuk pembahasan teoty dan analisis statistik selanjutnya.
















4. Kuartil (Q)
 a. kuartil information tunggal
   Langkah-langkah yang tempuh untuk mencari kuartil :
     - Susunan information menurut ururannta
     - Tentukan letak Kuartil
     - Tentukan nilai kuartilnya
    Rumus letak kuartil ke-i :




contoh:
Tentukan nilai quarti dari information berikut ini :
1,6,9,3,5,8,10

Jawab :
kita urutkan information terlebih dahulu menjadi 1,3,5,6,8,9,10






 b. Kuartil information berkelompok
Rumus :











Contoh :
Tentukan Q1 dari tabil di bawah :
Jawab :
Untuk Q1, maka i = 1
n = Jumlah seluruh frekuensi = 80
Letak Q1 = (1/4)n = (1/4)80 = 20
sehingga letak Q1 pada interval ke-3, yaitu xl - 44, maka :
Tb1 = xl - 0,5 = 39,5
f1    = 13
F1   = 8 + 10 = 18
c     = 35 - xxx = 5





c. Jangkauan Kuartil.dan Simpangan kuartil
Dari sekumpulan information yang mempunyai kuartil bawah Q1 dan kuartil atas Q3, Jangkauan kuartil dan simpangan kuartil adalah sebagai berikut :
Untuk contoh bisa kalian cari sendiri soalnya mudah ko

5. Desil (D)
a.Desil Data Tunggal
Kumpulan information yang di bagi 10 bagian yang sama, maka diperoleh sembilan pembagi dan tiap pembagi dinamakan desil.
Cara untuk menentukan desil :
    - Susunlah information menurut urutan nilainya
    - Tentukan letak desilnya
    - Hitung nilai desilnya
Letak desil ke-i dapat di tentukan dengan rumus :
Lokasi Di = information ke-(i(n + 1) / 10)










6. Persentil (P)
kumpulan information yang dibagi menjadi 100 bagian yang sama, maka di peroleh 99 pembagi dan tiap pembagi dinamakan persentil.
cara untuk mendapatkan persentil :
a. susunlah information menurut urutan nialinya
b. Tentukan letak persentilnya
c. Hitung nilai persentilnya

Letak persentil ke-i dapat di tentunkan dengan rumus berikut :

 Rumus presentil untuk information kelompok :











7. Angka Baku
Angka baku digunakan untuk mengetahui perbedaan suatu kejadian dibanding dengan kebiasaannya. Semakin besar angka bakunya semakin baik nilai tersebut dibandingkan dengan nilai yang lain yang memiliki angka baku lebih kecil.
Rumus :










Contoh :
diketahui : information : 2,7,8,10,4,dan5
                   rata-rata hitung : 6
                   Simpangan baku : akar 7
Tentukan angka baku dari 2!
jawab :












8. Koefisien Variansi (KV)
Koefisien variansi adalah perbandingan antara simpangan baku dengan rata-rata suatu information dan dinyatakan dalam%
Rumus :










Contoh :
lampu neon rata-rata dapat dipakai selama 2.800 jam dengan simpangan baku 700 jam, sedangkan lampu pijar dapat dipakai rata-rata selama 3.500 jam dengan simpangan  baku 1.050 jam. dara information di atas manakah yang lebih baik.
Jawab :








dari perhitungan koefisien variansi, lampu neon lebih baik dari lampu pijar, karena KV neon < KV lampu pijar


Nah segini yh materi dari saya
Untuk menambah pemahaman baca juga artikel tentang :
asalamualaikum goodbye bye.......

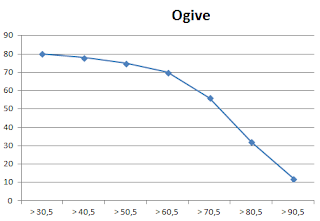
Cara Membuat Dan Menyajikan Tabel Distribusi Relatif Dan Kumulatif Beserta Ogiv, Histogram, Dan Poligon Frekuensinya.

Apa kabar guys???

kli ini gw punya ilmu tentang cara membuat tabel distribusi relatif dan kumulatif.
Simak ya!!!!!

Jika banyaknya frekuensi pada tiap interval dibandingkan denga jumlah information keseluruhan dan dinyatakan dalam bentuk persen, maka akan didapat frekuensi relatif (f rel.).
Contoh tabel distribusi frekuensi :

Rumus : f rel-... = (frekuensi ke...(f-..)/jumlah seluruh data(n))x100%
Dari tabel di atas frekuensi relatif interval pertamanya adalah
f rel-1 = (2/80)x100% = 2,5%
dan untuk yang ke dua dan seterusnya dengan cara yang sama juga :
f rel-2 = (3/80)  x100% =   3,75%
f rel-3 = (5/80)  x100% =   6,25%
f rel-4 = (14/80)x100% = 17,50%
f rel-5 = (24/80)x100% = 30.00%
f rel-6 = (20/80)x100% = 25,00%
f rel-7 = (12/80)x100% = 15,00%

Maka kita masukan f rel ke tabel :

Kemudian kita buat tabel frekuensi kumulatifnya.
Ada dua frekuensi kumulatif :
1. Frekuensi kumulatif kurang dari adalah frekuensi yang diperoleh dari jumlah frekuensi yang kurang dari atau sama dengan tepi atas kelas yang bersangkutan.
Tabel frekuensi kumulatif kurang dari :



kemudian kita membuat grafik dari frekuensi kumulatif kurang dari tersebut ( Ogive ).



2. Frekuensi kumulatif lebih dari adalah diperoleh dari jumlah frekuensi yang lebih atau sama dengan tepi bawah kelas yang bersangkutan.
Tabel frekuensi kumulatif lebih dari :
Ogive frekuensi kumulatif lebih dari :


Catatan ; ingat setiap grafik yang menunjukan frekuensi kumulatif di sebut Ogive

Nah sampe sini dulu yah meteri dari gw
Untuk menambah pemahaman baca juga artikel tentang :
Asalamualaikum farewell bye.....

Macam - Macam Diagram Dalam Ilmu Statistik

Nih guys macam - macam diagram :

1. Diagram Garis
 Untuk menggambarkan keadaan yang berkesinambungan atau kontinu maka dengan cara membuat diagram garis
Contoh :

2. Diagram Batang
Seperti halnya pada diagram garis, untuk information yang variablenya berbentuk kategori atau atribut (mempunyai ciri-ciri khusu) dapat disajikan dalam bentuk diagram batang.
Contoh :

3, Diagram lingkaran
Pada penyajian information dalam betuk diagram lingkaran, lingkaran di bagi dalam bentuk juring-juring lingkarang sesuai dengan information yang bersangkutan. Luas masing-masing juring sebanding dengan prosentase information yang bersangkutan

Contog :


4. Piktogram
Piktogram ialah diagram berbentuk gambar. Setiap gambar digunakan sebagai satua. Misalya i orang mewakili M jiwa.
contoh :

5. Histogram
Histogram merupakan diagram  untuk menyajika information dalam bentuk distribusi frekuensi. Sumbu tegak untuk menyatakan frekuensi dan sumbu mendatar untuk menyatakan batas interval kelas.
Contoh :


Nah guys sekian dulu yah materi dari gw 
Untuk menambah pemahaman baca juga artikel tentang :
asalamualaikum farewell bye....

Cara Mengumpulkan Information Dalam Ilmu Statistik

How are u guys ?????
I promise u fine, right!!!!
Heheheheh :D
Nah guys kali ini gw punya artikel beberapa cara pengumpulann information nih :       

1. Penelitian langsung di lapangan atau laboratorium.
     Penelitian di lapangan biasanya disebut dengan observasi atau pengamatan merupakan teknik pengumpulan information dengan cara pengamatan terhadap objek, baik secara langsung maupun tidak langsung, misalnya penelitian terhadap situs-situs purbakala dan penelitian di dalam laboraturium. Pengamatan dapat dilakukan dengan :
  1. Pengamatan langsung, yaitu pengamatan yang dilakukan tanpa perantara (secara langsung) terhadap objek yang diteliti.
  2. Pengamatan tak langsung, yaitu pengamatan yang dilakukan terhadap objek melalui perantara suatu alat atau cara.
  3. Pengamatan partisipasif, yaitu pengamatan yang dilakukan dengan cara ikut ambil bagian atau melibatkan diri dalam situasi yang dialami oleh responden. Cara ini banyak dilakukan terutama dalam penelitian psikologi, sosiologi, maupun antropologi.
2.Interview (wawancara)
     Teknik pengumpulan information yang dilakukan dengan cara mengadakan tanya jawab, baik secara langsung maupun tidak langsung dengan responden. Pada wawancara langsung, peneliti mengadakan tatap muka langsung dengan responden, sedangkan pada wawancara tidak langsung, peneliti mewawancarai perantara tahu persis tentang objek yang diteliti.

 3.Kuesioner (Angket)
     Angket dapat dipandang sebagai teknik pengumpulan information yang banyak kesamaannya dengan wawancara. Perbedaannya adalah wawancara dilakukan secara lisan, sedangkat angket dilakukan secara tertulis. Bentuk penyusunan angket ada dua macam, yaitu :

  1.  Angket berstruktur, yaitu angket yang menyediakan kemunkinan jawaban.
  2.  Angket tak berstruktur, yaitu angket yang tidak menyediakan kemungkinan jawaban.
                                                  contoh angket :


Nah segini dulu yah guys materi dari gw
Untuk menambah pemahaman baca juga artikel tentang :
Assalamualaikum Bye bye………………………..

Kamus Matematika Hampir Lengkap

Hallo temen-temen???
Pertama-tama gue ucapin trimakasih buat para pengunjung weblog gue :). Slamat datang di weblog paling bermanfaat sedunia.
Dan gue doaian semoga orang-orang yang ngunjungin weblog gue pada masuk surga semua, trs selama hidupnya selalu di beri kemudahan, trs all the best deh buat kalian :D
Udah kaya ulang tahun aja ya ???.... Sorry ya klo penulis suka bercanda :)
Kembali lagi bersama gue muhamad pajar sidik, gue adalah seorang penulis blogger yang ganteng dan baik hati :D cieeee.....
Di hari yang indah ini alhamdulillah gue bisa nulis artikel kembali, yang mudah-mudahan artikel ini bisa bermanfaat buat kalian semua.
Kali ini gue bakalan nulis artikel tentang Kamus Matematika Hampir Lengkap, Tanpa panjang lebar lagi yo depository fiscal establishment gibe it out !
Kamus Matematika Hampir Lengkap

Kamus Matematika Hampir Lengkap


Fungsi

Domain
:
Daerah asal
Fungsi kuadrat
:
fungsi dengan bentuk f(x) = ax2 + bx + c
Fungsi linear
:
fungsi dengan bentuk f(x) = ax + b
Kodomain
:
Daerah kawan
Range
:
Daerah hasil

Logika Matematika

Biimplikasi
:
kalimat majemuk yang dihubungkan dengan kata "jika dan hanya jika"
Disjungsi
:
Kalimat majemuk yang dihubungkan dengan kata "atau"
Implikasi
:
kalimat majemuk yang dihubungkan dengan kata "jika ... maka ... "
Konjungsi
:
kalimat majemuk yang dihubungkan dengan kata "dan/tetapi"
Kontradiksi
:
tabel kebenaran pernyataan majemuk yang bernilai salah semua
Negasi
:
Ingkaran
Tautologi
:
tabel kebenaran pernyataan majemuk yang bernilai benar semua

Matematika Keuangan

Aktiva
:
Segala sumber daya ekonomi dari suatu prusahaan yang berupa harta maupun hak-hak yang dimiliki berdasarkan kekuatan hukum
Anuitas
:
Sejumlah pembayaran pinjaman yang sama besarnya. Yang dibayarkan setiap jangka waktu tertentu. dan terdiri atas bagian bunga dan bagian angsuran
Bunga
:
Jasa dari pinjaman
Bunga Majemuk
:
Proses bunga berbunganya suatu modal
Bunga tunggal
:
Bunga yang diperoleh pada setiap akhir jangka waktu tertentu yang tidak mempengaruhi besarnya modal yang dipinjam
Depresiasi
:
Perkurangnya nilai ekonomi suatu aktiva
Diskonto
:
Bunga yang dibayarkan oleh peminjam pada saat menerima pinjaman
Obligasi
:
Surat berharga yang merupakan perjanjian pinjaman tertulis
Persen di atas 100
:
Bentuk pecahan yang selisih antara penyebut dan pembilangnya sama dengan seratus
Persen di bawah 100
:
Bentuk pecahan yang jumlah antara penyebut dan pembilangnya sama dengan seratus
Rente
:
Sederetan modal atau angsuran yang dibayarkan atau diterima pada setiap jangka waktu tertentu yang tetap besarnya
Rente kekal
:
Rente yang jumlah angsurannya tidak terbatas
Rente postnumerando
:
Rente yang dibayarkan atau diterima di akhir periode
Rente pranumerando
:
Rente yang dibayarkan atau diterima di awal periode

Matriks

Matriks
:
susunan elemen-elemen atau entri-entri yang berbentuk persegi panjang yang diatur dalam baris dan kolom
Matriks diagonal
:
matriks yang seluruh elemennya nol kecuali pada diagonal utamanya tidak semuanya nol
Matriks identitas
:
matriks yang semua elemen pada diagonal utamanya adalah satu dan elemen lainnya adalah no
Matriks singular
:
matriks yang harga determinannya = o atau matriks yang tidak memiliki invers
Minor
:
determinan submatriks yang tinggal setelah baris ke-i dan kolom ke-j dicoret dari A
Ordo matriks
:
Banyaknya elemen baris diikuti banyaknya kolom
Transpose matriks
:
mengubah susunan matriks dari baris menjadi kolom atau sebaliknya

Peluang

Frekuensi harapan
:
Hasil kali peluang P(A) dengan banyknya percobaan n
Hasil kejadian
:
Himpunan bagian dari ruang sampel
Kaidah pencacahan
:
Suatu kaidah yang digunakan untuk menentukan atau menghitung berapa banyak cara yang terjadi dari suatu peristiwa
Kejadian majemuk
:
Kejadian yang dibentuk dengan cara menggunakan dua atau lebih kejadian sederhana
Kejadian saling bebas
:
Apabila kemunculan kejadian yang satu tidak dipengaruhi oleh kemunculan kejadian lainnya
Kombinasi
:
Susunan k obyek dengan urutan tidak diperhatikan dari n obyek yang tersedia
Komplemen A
:
Banyaknya kejadian yang bukan A
n faktorial
:
Hasil kali bilanga n bulat positif dari 1 sampai dengan n
Permutasi
:
Susunan k obyek yang berbeda dari n obyek yang tersedia dimana
Ruang sampel
:
Peristiwa yang mungkin muncul dari suatu percbaan

Persamaan dan Pertidaksamaan

Akar-Akar persamaan kuadrat
:
penyelesaian persamaan kuadrat
Diskriminan
:
pembeda persamaan kuadrat
Eliminasi
:
melenyapkan
Persamaan
:
kalimat terbuka yang memuat tanda "sama dengan"
Persamaan atau pertidaksamaan linear
:
suatu persamaan atau pertidaksamaan dengan variabelnya berpangkat satu
Persamaan kuadrat
:
persamaan dimana pangkat tertinggi dari variabel (peubah) adalah dua
Pertidaksamaan
:
kalimat terbuka yang memuat tanda "<, <, >, >"
Subtitusi
:
mengganti atau menyatakan salah satu variabel dengan variabel lainnya

Program Linier

Garis selidik
:
suatu garis yang digunakan untuk menyelidiki nilai optimum (maksimum atau minimum) yang diperoleh dari sungsi sasaran atau fungsi objektif.
Model matematika
:
suatu rumusan (dapat berupa persamaan pertidaksamaan atau fungsi) yang diperoleh dari suatu penafsiran ketika menterjemahkan suatu soal verbal
Nilai optimum
:
maksimum atau minimum
Program linear
:
cara untuk menyelesaikan suatu peroalan (penyelesaian optimum) dengan menggunakan metode matematik yang dirumuskan dalam bentuk persamaan-persamaan atau pertidaksamaan-pertidaksamaan linear

Skema Bilangan Rill

Bentuk akar
:
akar atau suatu bilangan yang nilainya merupakan bilangan irasional
Bilangan berpangkat
:
a pangkat n didefinisikan dengan a x a x a x ... x a (sampai n suku)
Bilangan komposit
:
bilangan yang memiliki faktor lebih dari dua
Bilangan rasional
:
bilangan yang dapat dibentuk menjadi a/b dengan b tidak sama dengan 0
Bilangan real
:
terdiri atas dua jenis bilangan yaitu bilangan rasional dan irasional
Indeks
:
bilangan bulat dari hasil pengambilan logaritma
Logaritma
:
a pangkat c sama dengan b identik dengan a log b = c
Mantise
:
bilangan desimal dari hasil pembilang logaritma
Perbandingan Berbalik nilai
:
dua perbandingan yang harganya saling berbalikan
Perbandingan senilai
:
dua perbandingan yang nilainya sama
Persen
:
pembagian dengan seratus
Skala
:
bentuk perbandingan senilai dari ukuran suatu besaran nyata

Statistika

Angka Baku
:
Nilai yang menyatakan perbandingan antara selisih information dengan rata-ratanya dengan simpangan baku information tersebut
Data
:
Sekumpulan keterangan yang dapat menjelaskan sesuatu hal
Desil
:
Nilai information yang membagi information menjadi 10 bagian sama besar setelah information diurutkan
Deskriptif
:
Gambaran suatu information apa adanya
Foligon frekuensi
:
Diagram garis yang tertutup yang diperoleh dari daftar distribusi frekuensi
Histogram
:
Diagram batang yang saling berimpit yang diperoleh dari daftar distribusi frekuensi
Inferensial
:
Kegiatan statistika dimulai dari pengumpulan information sampai pada pengambilan keputusan secara logis dan rasional
Interview
:
Pengumpulan information melalui wawancara
Koefisien Variasi
:
perbandingan antara simpangan baku dengan rata-rata suatu information dan dinyatakan dalam %.
Kuartil
:
Nilai information yang membagi information menjadi four bagian sama besar setelah information diurutkan
Kuesioner
:
Pengumpulan information melalui angket
Mean
:
Rata-rata hitung
Median
:
Nilai information yang terletak di tengan setelah information diurutkan
Modus
:
Nilai information yang sering muncul
Observasi
:
Pengumpulan information melalui pengamatan
Ogive
:
Diagram garis yang diperoleh dari daftar distribusi frekuensi kumulatif
Persentil
:
Nilai information yang membagi information menjadi 100 bagian sama besar setelah information diurutkan
Piktogram
:
Nama lain diagram lambang
Populasi
:
Keseluruhan information yang akan diteliti
Rata-rata simpangan
:
Perbandingan harga mutlak selisih information dengan rata-ratanya dengan banyaknya data
Reliabel
:
Kesalah buku kecil, dapat terpercaya
Representatif
:
Dapat mewakili
Simpangan baku
:
Ukuran depresiasi dengan rumus
Statistika
:
Pengetahuan yang berhubungan dengan pengumpulan data, penarikan kesimpulan dan pengambila keputusan secara logis dan rasional tentang information tersebut
Up to date
:
Terkini
Varians
:
Simpangan baku kuadrat

Sekian artikel kali ini. Oh iya bila ada teman-teman yang ingin menambahkan kosa kata pada kamus ini, silahkan saja langsung tuliskan pada kolom komentar di bawah. Mohon maaf apabila da salah-salah kata.
Akhir kata wassalamualaikum wr. wb.
Referensi :
  • Buku matematika SMK kelompok penjualan dan akuntansi karangan To'ali
Subscribe to: Posts (Atom)