Home Trigonometri Materi Trigonometri

Materi Trigonometri

Diterbitkan

Hallo para pengunjung weblog yang cantik dan juga ganteng ??? :)
Semoga sehat selalu ya
Kali ini saya akan berbagi materi tentang Trigonometri. Kebanyakan orang ktika mendengar kata matematika apalagi tentang trigonometri pasti mereka akan stress duluan :D, jusk kidding guys
Namun kalian jangan khawatir, karena saya akan menyajikan materi Trigonometri  dengan bahasa yang mudah kalian fahami dan dengan sedikit efek animasi yang ngga bisa dimilikin sama weblog lain. Sombong dikit hehehehe :D
Yu udah ngga sabar nih kita lanjut ke materi :)


Pengertian Trigonometri
Trigonometri berasal dari bahasa yunani yaitu trigonon dan metron.Trigonon adalah segita dan metron adalah perhitungan, jadi pengertian trigonometri adalah salah satu cabang ilmu matematika yang mempelajari tentang perhitungan segitiga, sudut-sudut segitiga, hubungan sudut dengan sisi pada segitiga, dan sebgainya. Lalu apa sajakah yang kita pelajari dalam trigonometi??? jika anda ingin menguasai ilmu trigonometri, simak uraian materi selanjutnya di bawah ini !!! :)

 Ukuran Sudut
Dalam Trigonometri ada yang namanya ukuran sudut. Ukuran sudut itu ada two :

1. Drajat
Drajat dalam ilmu matematika kita tuliskan dengan ( ° ). Ada tiga macam sudut pokok dalam matematika, diantaranya :
a. Sudut siku-siku yaitu 90° Hallo para pengunjung weblog yang cantik dan juga ganteng Materi Trigonometri
b. Sudut lurus yaitu 180° __
c. Sudut rotasi penuh 360°  Hallo para pengunjung weblog yang cantik dan juga ganteng Materi Trigonometri

2. Radian
Radian adalah ukuran sudut yang berkaitan dengan radius . Perhatikan gambar di bawah !

Apabila sudut pokok kita hitung dalam radian maka :
a. Sudut siku-siku yaitu π/2 Hallo para pengunjung weblog yang cantik dan juga ganteng Materi Trigonometri
b. Sudut lurus yaitu π __
c. Sudut rotasi penuh 2π  Hallo para pengunjung weblog yang cantik dan juga ganteng Materi Trigonometri

 3. Mengubah Drajat Ke Radian
Ukuran sudut dalm drajat mungkin banyak salah satu dari kita yang sering menggunakan dan mungkin juga sudah mahir dengan menggunakan drajat, namun perlu kita ketahui ukuran sudut juga tidak hanya derajat saja akan tetapi ada yang namanya radian. Lalu bagaimana caranya mengubah drajat ke radian, perhatikan rumus di bawah !
Maka untuk mengubah drajat ke radian berlaku rumus : q/180° x π, dengan q adalah nilai drajatnya
Contoh :
Berapa radiankah nilai dari 30° ???
Jawab :
q/180° x π = 30°/180° x π = 1/6 x π = 1/6π Radian 

 4. Mengubah Radian Ke Drajat
Untuk mengubah radian ke drajat berlaku rumus : R/π x 180°,  dengan R adalah nilai radiannya
Contoh :
Berapakah drajatkah nilai dari three radian??
Jawab :
R/π x 180° = 3/π x 180° = 540°/π  


Perbandingan Trigononmetri Pada Segitiga Siku-Siku
Pada segitiga siku-siku ini kita harus mengenal dulu istilah Hypotenuse, Opposite, dan Adjacent.


Dalam perbandingan sisi dan sudut pada segitiga dikenal sinus, cosinus, dan tangen.
Rumus Sinus     : sin  q = opposite / hypotenuse
Rumus Cosinus : cos q = Adjacent / hypotenuse
Rumus Tangen  : tan q = opposite / Adjacent

Contoh :
Tentukan berapa nilai sinus, cosinus, dan tangen dari gambar di samping !
Jawab :
Hypotenuse : 4,9
Opposite      : 2,8
Adjacent.     : 4,0
sin  30° = opposite / hypotenuse = 2,8 / 4,9 = 0,57
cos 30° = Adjacent / hypotenuse = 4,0 / 4,9 = 0,81
tan 30° = opposite / Adjacent = 2,8 / 4,0 = 0,7

Selain sinus(sin), cosinus(cos), dan tangen(tan). Ada juga yang namanya cosecant (csc), secant (sec), dan cotangent (cot). Cosecant , Secant , dan Cotangent  merupakan kebailkan dari sinus, cosinus, dan tangen.
Rumus Cosecant     : csc  q = hypotenuse / opposite
Rumus Secant         : s  q = hypotenuse / Adjacent
Rumus Cotangent   : cot  q = Adjacent / opposite

Contoh :
Tentukan berapa nilai Cosecant, secant, dan cotangen dari gambar di samping !
Jawab :
Hypotenuse : 4,9,  Opposite: 2,8,  Adjacent.: 4,0
csc  30° = hypotenuse / opposite = 4,9 / 2,8 = 1,75
s  30° = hypotenuse / Adjacent = 4,9 / 4,0 = 1.225
cot  30° = Adjacent / opposite = 4,0/ 2,8 = 1.428
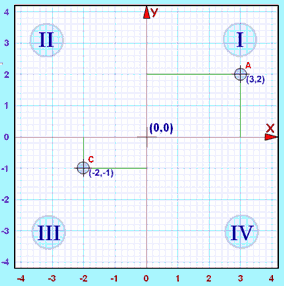
Letak Kuadran 
Dalam satu putaran, yaitu 360°, sudut dibagi menjadi empat relasi, yaitu:
1. Kuadran I   : 0°≤ α ≤ 90°
2. Kuadran II  : 90° < α ≤ 180°
3. Kuanran III : 180° < α ≤ 270°
4. Kuadran IV : 270° < α ≤ 360°
  • Pada Kuadran I sumbu x bernilai (+) dan sumbu y bernilai positif (+)
  • Pada Kuadran II sumbu x bernilai negatif (-) dan sumbu y bernilai positif (+)
  • Pada Kuadran III sumbu x bernilai negatif (-) dan sumbu y bernilai negatif (-)
  • Pada Kuadran IV sumbu x bernilai positif (+) dan sumbu y bernilai negatif(-)


Persamaan Trigonometri
1. Persamaan Pada Sinus
Pada persamaan sinus berlaku :
sin x° = sin a° ® x = a + k  x 360°® x = (180 - a) + k  x 360°

 2. Persaman Pada Cosinus
Pada persamaan cosinus berlaku :
cos x° = cos a° ® x = a + k  x 360°® x = - a + k  x 360°

3. Persamaan Pada Tangen
Pada persamaan tangen berlaku :
tan x° = tan a° ® x = a + k  x 180°

Identitas Trigonometri
Identitas segitigas siku-siku. Untuk mengetahui identitas segitiga siku-siku perhatika gambar di bawah :

Dari gambar di atas terliha bahwa :
Adjacent selalu terletak setelah sudut
Opposite slalu terletak tanpa menyentuh sudut.
Dan Hypotenuse merupakan sisi terpanjang pada segitiga.

Identitas pada sin, cos, dan tan, Rumus sin, cas, dan tan :
Rumus Sinus     : sin  q = opposite / hypotenuse
Rumus Cosinus : cos q = Adjacent / hypotenuse
Rumus Tangen  : tan q = opposite / Adjacent

Jika :

Maka : tan q = sin  q / cos q

Identitas pada csc, sec, dan cot, Rumus csc, sec, cot :
Rumus Cosecant     : csc  q = hypotenuse / opposite
Rumus Secant         : s  q = hypotenuse / Adjacent
Rumus Cotangent   : cot  q = Adjacent / opposite

Sebenernya csc, sec, dan cot merupakan kebalikan dari sin, cos, dan tan. Maka :
sin(θ) = 1/csc(θ)
cos(θ) = 1/sec(θ)
tan(θ) = 1/cot(θ)
Adapun rumus lain :
cot  q = cos q / sin  q

Sekian dulu ya materi dari saya assalamualaikum wr. wb.
Saya sarankan baca juga artikel :

Share to your friends

Artikel Terkait

raven

Next Post
Previous Post