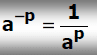Home Posts filed under Search results for aturan-dasar-bilangan-berpangkat
Showing posts sorted by relevance for query aturan-dasar-bilangan-berpangkat. Sort by date Show all posts
Showing posts sorted by relevance for query aturan-dasar-bilangan-berpangkat. Sort by date Show all posts

Aturan Dasar Bilangan Berpangkat

Hallo temen-temen???
Pertama-tama gue ucapin trimakasih buat para pengunjung weblog gue :). Slamat datang di weblog paling bermanfaat sedunia.
Dan gue doaian semoga orang-orang yang ngunjungin weblog gue pada masuk surga semua, trs selama hidupnya selalu di beri kemudahan, trs all the best deh buat kalian :D
Udah kaya ulang tahun aja ya ???.... Sorry ya klo penulis suka bercanda :)
Kembali lagi bersama gue muhamad pajar sidik, gue adalah seorang penulis blogger yang ganteng dan baik hati :D cieeee.....
Di hari yang indah ini alhamdulillah gue bisa nulis artikel kembali, yang mudah-mudahan artikel ini bisa bermanfaat buat kalian semua.
Kali ini gue bakalan nulis artikel tentang Aturan Dasar Bilangan Berpangkat, Tanpa panjang lebar lagi yo depository fiscal establishment check it out !
Terdapat aturan aturan yang harus diketahui dulu untuk menyelesaikan soal, diantaranya :

1. Aturan Perkalian Bilangan Berpangkat dengan Bilangan Pokok Yang Sama

Ketarangan :
a : Sebuah Bilangan
p dan q : Pangkat pada sebuah bilangan

Contoh :
Berapakah hasil dari 52 x 53 ???
Jawab :
Dengan menggunakan rumus aturan perkalian bilangan berpangkat dengan bilangan pokok yang sama, maka a = 5, p = 2, dan q = three kita masukan ke dalam rumus tersebut :
ap x aq  = ap + q
52 x 53  = 52 + 3
52 x 53  = 55

2. Aturan Pembagian Pada Bilangan Berpangkat dengan Bilangan Pokoknya Sama

Ketarangan :
a : Sebuah Bilangan
p dan q : Pangkat pada sebuah bilangan

Contoh :
Berpakah hasil dari 53 : 52 ???
Jawab :
Dengan menggunakan rumus aturan pembagian bilangan berpangkat dengan bilangan pokok yang sama, maka a = 5, p = 3, dan q = ii kita masukan ke dalam rumus tersebut :
ap : aq  = ap - q
53 : 52  = 53 - 2
53 : 52  = 51

3. Aturan Pemangkatan Pada Bilangan Berpangkat

Ketarangan :
a : Sebuah Bilangan
p dan q : Pangkat pada sebuah bilangan

Contoh :
Berapakah hasil dari (52)3????
Jawab :
Dengan menggunakan rumus aturan pemangkatan pada bilangan berpangkat, maka a = 5, p = 2, dan q = three kita masukan ke dalam rumus tersebut :
(ap)q  = ap x q
(52)3  = 52 x 3
(52)3  = 56

4. Aturan Pemangkatan dari Perkalian Dua Bilangan

Ketarangan :
a dan b : Sebuah Bilangan
p : Pangkat pada sebuah bilangan 

Contoh :
Berapakah hasil dari (2 x 3)4 ???
Jawab :
Dengan menggunakan rumus aturan pemangkatan dari perkalian dua bilangan, maka a = 2, b = 3, dan p = iv kita masukan ke dalam rumus tersebut :
(a x b)p  = ap x bp
(2 x 3)4  = 24 x 34
(2 x 3)4  = 24 x 34

5. Aturan Pemangkatan dari Pembagian Dua Bilangan

Ketarangan :
a dan b : Sebuah Bilangan
p : Pangkat pada sebuah bilangan 

Contoh :
Berapakah hasil dari (2 : 3)4 ????
Jawab :
Dengan menggunakan rumus aturan pemangkatan dari pembagian dua bilangan, maka a = 2, b = 3, dan p = iv kita masukan ke dalam rumus tersebut :
(a : b)p  = ap : bp
(2 : 3)4  = 24 : 34
(2 : 3)4  = 24 : 34

6. Aturan Bilangan Berpangkat Negatif

Ketarangan :
a : Sebuah Bilangan
p : Pangkat pada sebuah bilangan

Contoh :
Berapakah hasil dari 2-3 ???
Jawab :
Dengan menggunakan rumus Aturan Bilangan Berpangkat Negatif, maka a = 2, dan p = three kita masukan ke dalam rumus tersebut :
a-p  = 1/ap
2-3 = 1/23

7. Aturan Pemangkatan Bilangan Pecahan

Ketarangan :
a : Sebuah Bilangan
p dan q : Pangkat pada sebuah bilangan

Contoh :
Berapakah hasil dari 23/4 ???
Jawab :
Dengan menggunakan rumus Aturan Pemangkatan Bilangan Pecahan, maka a = 2, p = 3, dan q = iv kita masukan ke dalam rumus tersebut :
ap/q = q√ap
23/4 = 4√23

Kesimpulan

Jadi sebelum teman-teman mempelajari lebih dalam tentang bilangan berpangkat, teman-teman harus memahami aturan-aturannya operasi bilangan berpangkat terlebih dahulu diantaranya :
  1. Aturan Perkalian Bilangan Berpangkat dengan Bilangan Pokok Yang Sama
  2. Aturan Pembagian Pada Bilangan Berpangkat dengan Bilangan Pokoknya Sama
  3. Aturan Pemangkatan Pada Bilangan Berpangkat
  4. Aturan Pemangkatan dari Perkalian Dua Bilangan
  5. Aturan Pemangkatan dari Pembagian Dua Bilangan
  6. Aturan Bilangan Berpangkat Negatif
  7. Aturan Pemangkatan Bilangan Pecahan
Nah segini dulu ya artikel kali ini. Mohon maaf apabila ada salah - salah kata
Baca juga artikel tentang :
Akhir kata wassalamualaikum wr. wb.

Bilangan Berpangkat

Pengertian Bilangan Berpangkat
Bilangan berpangkat ialah bilangan yang memiliki nilai pangkat. Bilang berpangkat di temukan oleh John Napier seorang bangsawan Merchiston, Scotlandia.
Rumus Bilangan Berpangkat :
an = a x a x a x…..x a (sampai n factor)
Contoh :
  23  = two x two x two = 8
-23 = -2 x (-2) x (-2) = -8

Aturan Dasar Bilangan Berpangkat :
1. Bilangan Berpangkat 0
Apabila setiap bilangan dipangkatkan dengan 0 maka hasilnya adalah 1 atau a0 = 1
Contoh Bilangan Berpangkat 0 :
-20 = 1
 50 = 1

2. Bilangan Berpangkat Negatif.
Apabila setiap bilangan dipangkatkan denga bilang negatif maka a-n = 1/an
Contoh Bilangan Berpangkat Negatif :
2-3 =  1/23  = 1/2 x 1/2 x 1/2 = 1/8

3. Bilangan Berpangkat Pecahan.
Apabila bilangan dipangkatkan dengan bilangan pecahan maka an/m = m√an 
Contoh Bilangan Berpangkat Pecahan :
24/2 = 2√24  = 2√16 = 4

Sifat Bilangan Berpangkat Bulat Positif
1. an x am = an+m  , a bilangan existent dan m,n bilangan bulat positif.
2. an : am = an-m  , a ¹ 0 dan n > one thousand
3. (an)m = an x m , a bilangan existent dan m,n bilangan bulat positif.
4. (a x b)n = an x bn , a,b bilangan existent dan n bilangan bulat positif.
5. (a : b)m = am : bm, a,b bilangan existent dan one thousand bilangan bulat positif.

Contoh Soal Sifat Bilangan Berpangkat :
1. 24 x 23 = 24+3 = 27
2. 24 : 23 = 24-3 = 21
3. (24)3 = 24x3 = 212
4. (2 x 8)4 = 24 x 84
5. (2 : 8)4 = 24 : 84

Persamaan Bilangan Berpangkat
Dalam persamaan bilangan berpangkat ini kita akan menyamakan dua bilangan berpangkat dan yang menjadi objek yang kita cari ialah pangkat dari bilangan tersebut atau variable dari pangkat bilangan tersebut.

Contoh Persamaan Bilangan Berpangkat :
Tentukan harga x yang memenuhi persamaan eksponen 22x = 64!
Jawab :
22x = 64, 64 bisa kita sederhankan menjadi 26
22x = 26 , karena bilangan yang dipangkatkannya sama yaitu 2, maka kita hilangkan saja alias core.
2x = half-dozen , supaya ruas kana menjadi x saja, maka kita bagi kedua ruah dengan 2.
2x/2 = 6/2
x = 3
Maka kita telah memecahkan soalnya yaitu x yang memenuhi persamaan  22x = 64 adalah 3

Soal spesial untuk kalian :
Berpakah sisa dari 321 dibagi oleh 10????
yang bisa menjawabnya berarti kalian pintar

Nah segini dulu ya materi dari saya
mohon maaf jika ada kesalahan
kritik, komentar, pesan, dan pertanyaan saya tunggu di komntar ok
untuk melanjutkan materi saya sarankan untuk membaca materi tentang :
Baca juga artikel tentang :
assalamualaikum wr. wb.

Operasi Bilangan Berpangkat Tak Sebenarnya

Hallo temen-temen???
Pertama-tama gue ucapin trimakasih buat para pengunjung weblog gue :). Slamat datang di weblog paling bermanfaat sedunia.
Dan gue doaian semoga orang-orang yang ngunjungin weblog gue pada masuk surga semua, trs selama hidupnya selalu di beri kemudahan, trs all the best deh buat kalian :D
Udah kaya ulang tahun aja ya ???.... Sorry ya klo penulis suka bercanda :)
Kembali lagi bersama gue muhamad pajar sidik, gue adalah seorang penulis blogger yang ganteng dan baik hati :D cieeee.....
Di hari yang indah ini alhamdulillah gue bisa nulis artikel kembali, yang mudah-mudahan artikel ini bisa bermanfaat buat kalian semua.
Kali ini gue bakalan nulis artikel tentang Operasi Bilangan Berpangkat Tak Sebenarnya, Tanpa panjang lebar lagi yo depository fiscal establishment check it out !

1. Perpangkatan dari Akar Suatu Bilangan

Untuk menentukan hasil pemangkatan dari akar suatu bilangan dapat digunakan sifat-sifat dari pemangkatan suatu bilangan, yaitu :
a x a = a2
(a + b)2 = a2 + 2ab + b2
(a - b)2 = a2 - 2ab + b2

Contoh :

  1. (√5)2 = √5 x √5
    (√5)2 = √52 = 5
  2. (√3)-3 = 1/√3 x 1/√3 x 1/√3
    (√3)-3 = 1/√3 x √3 x 1/√3
    (√3)-3 = 1/3√3
  3. (√3 +√2)2 = (√3)2 + 2(√3)(√2) +(√2)2
    (√3 +√2)2 = three + 2√6 +2
    (√3 +√2)2 = v + 2√6
  4. (√5 + 2)2 = (√5)2  - 2(√5)(2) +22
    (√5 + 2    )2 = v - 4√5 + 4
    (√5 + 2    )2 = nine - 4√5

2. Penjumlahan dan Pengurangan Bilangan Berpangkat Tak Sebenernya

Contoh :
  1. 2√5 + 3√5 = (2+3)√5 = 5√5 atau 51 x 51/2 = 53/2
  2.  32/3 + 3/2/3 = 3√32 + 3√32 =  2(3√32) = 2(32/3)
  3. 2  x 31/5 - 5√3 = ii x 5√3 - 5√3 = 5√3 = 31/5
  4. 4√2 - 2√2 = 2√2 = 21/2   

3. Perkalian dan Pembagian Bilangan Berpangkat Tak Sebenarnya

Sebenarnya belajar perkalian dan pembagian bilangan berpangkat tak sebenarnya, ingatlah terlebih dahulu perkalian dan pembagian bilangan berpangkat sebenaarnya, yaitu :
am x an = am+n
am : an = am-n
Sifat-sifat di atas juga berlaku untuk perkalian dan pembagian pada bilangan berpangkat tak sebenarnya.
Contoh :
  1. 32/3 x 31/2 = ……
    Jawab :
    32/3 x 31/2 = 3(2/3 )+( 1/2)
    32/3 x 31/2 = 3(4/6) +(3/6)
    32/3 x 31/2 = 37/6
    32/3 x 31/2 = 6√37
    32/3 x 31/2 = 6√(36 x 3)
    32/3 x 31/2 = three 6√36
  2.  5-1/2 : 5-1/3 = …
    Jawab :
    5-1/2 : 51/3 = 5(-1/2) -(1/3)
    5-1/2 : 51/3 = 5(-3/6) -(2/6)
    5-1/2 : 51/3 = 5(-5/6)
    5-1/2 : 51/3 = 1/5(5/6)
    5-1/2 : 51/3 = 1/6√55

4. Pemangkatan Bilangan Berpangkat Tak Sebenarnya

Ingatlah, pemangkatan bilangan yang berpangkat sebenarnya, yaitu :
(am)n = a(mxn) = amn
Rumus di atas juga berlaku untuk pemangkatan bilangan berpangkat tak sebenarnya.
Contoh :
  1. (32/3)6 = ….
    Jawab :
    (32/3)6 = 3(2/3) x 6
    (32/3)6 = 34
    (32/3)6 = 81
  2.  (√63)2/3 = …
    Jawab :
    (√63)2/3 = 6(3/2) x (2/3)
    (√63)2/3 = 66/6
    (√63)2/3 = 61
    (√63)2/3 = 6
  3.  (51/2)-4 = …..
    Jawab :
    (51/2)-4 = 5(1/2) x (-4)
    (51/2)-4 = 5-2
    (51/2)-4 = 1/52
    (51/2)-4 = 1/25

v Menggunakan Kalkulator dalam Menentukan Nilai Bilangan dengan Pangkat Tak Sebenarnya

Dalam menentukan nilai bilangan dengan pangkat tak sebenarnya, kalian dapat menggunakan kalkulator. Kalkulator yang digunakan adalah kalkulator ilmiah  (Scientific Calculator).
Langkah - langkah penggunaan adalah :
  1. Nyalakan kalkulator dengan menekan tombol On/C
  2. Tekan tombol bilangan yang akan ditentukan nilai pangkatnya.
  3. Tekan tombol x^y. Selanjutnya tekan tombol angka pembilang dari pangkat
  4. Tekan lagi tombol x^y. Tekan tombol angka yang merupakan penyebut dari pangkat.
  5. Takan tombol 1/x dan terakhir tekan tombol  =  . maka hasilnya akan tampak pada layar.
 Contoh :
Tentukan nilai dari bilangan berpangkat (27)2/3 ! 
Jawab :
(27)2/3 =.... tombol-tombol yang ditekan adalah :
Maka nilai yang tampak pada layar adalah 9
Nah segini dulu ya artikel kali ini. Mohon maaf apabila ada salah-salah kata
Baca juga artikel tentang :
Akhir kata wassalamualaikum wr. wb.

Subscribe to: Posts (Atom)